Riflessioni sulle Scienze

di Alberto Viotto    indice articoli

 

John Nash, Adam Smith ed il ruolo della legge

Febbraio 2015

• L'equilibrio di Nash

• La mano invisibile di Adam Smith

• L'ottimo di Pareto

• L'allocazione ottimale

John Forbes Nash, premio Nobel per l’economia nel 1994 e celebrato dal noto film ‘A beautiful mind’, è famoso soprattutto per i suoi contributi alla teoria dei giochi. Uno dei concetti fondamentali di questa teoria è l’‘equilibrio di Nash’.

 

L'equilibrio di Nash

In una situazione in cui più persone interagiscono si ha un ‘equilibrio di Nash’ se nessuna persona ha interesse a cambiare il proprio comportamento, indipendentemente dal comportamento degli altri – in pratica, se ognuno si comporta in modo egoistico e non collaborativo. Non sempre un ‘equilibrio di Nash’ corrisponde ad una situazione ottimale, come si può vedere nel caso del ‘dilemma del prigioniero’.

In questo famoso esempio, due prigionieri accusati dello stesso reato sono di fronte alla scelta tra parlare (accusando l'altro) o non parlare.

• Se nessuno dei due parla avranno entrambi una pena di 1 anno

• Se si accusano a vicenda avranno una pena di 6 anni

• Se uno solo parla avrà la libertà mentre l'altro avrà una pena di 7 anni

La scelta migliore per la ‘società’ composta dai due prigionieri sarebbe di non parlare, ma questa scelta non è un equilibrio di Nash: infatti uno qualsiasi dei due, se fosse il solo a parlare, potrebbe migliorare la sua situazione. Paradossalmente, l’unico equilibrio di Nash di questo esempio è la situazione peggiore per la ‘società’, quella in cui entrambi parlano prendendo 6 anni a testa.

Dal punto di vista del singolo prigioniero, infatti:

• Se il suo compagno non ha parlato, se lui stesso parla è libero invece di essere condannato ad un anno

• Se il suo compagno ha parlato, se lui stesso parla è condannato a 6 anni invece che a 7

A ciascuno dei due prigionieri conviene parlare; dal punto di vista dell’equilibrio di Nash è irrilevante il fatto che se un prigioniero parla peggiora la situazione dell’altro.

 

La mano invisibile di Adam Smith

Secondo la teoria economica ‘classica’ di Adam Smith (1723-1790), se ogni componente di un gruppo persegue il proprio interesse personale e vi sono condizioni di concorrenza perfetta, nell'equilibrio che ne esce ogni azione individuale accresce la ricchezza complessiva del gruppo (la nota metafora della ‘mano invisibile’). La teoria dei giochi dimostra che non è così: se ogni componente del gruppo fa ciò che è meglio per sé, il risultato cui si giunge è, in generale, un equilibrio di Nash che però non rappresenta la soluzione migliore per la ‘società’ e può inoltre rappresentare un'allocazione inefficiente delle risorse. Nel caso del dilemma del prigioniero il valore minimo possibile di anni di carcere è 0 per il singolo e 2 per il gruppo, ma se entrambi scelgono secondo il proprio esclusivo interesse ne ottengono 6 a testa.

 

L'ottimo di Pareto

Wilfredo Pareto (1848-1923) fu un famoso economista, noto per alcuni fondamentali concetti come quello di ottimo paretiano. Si ha un ‘ottimo paretiano’ quando si è raggiunta una situazione in cui non è possibile migliorare la condizione di una persona senza peggiorare la condizione di un’altra. L’ottimo paretiano si raggiunge se si collabora, a differenza che nell’equilibrio di Nash, anche se nessuno accetta di peggiorare neppure di poco la propria situazione.

Nel caso del dilemma del prigioniero si hanno tre ottimi paretiani, il caso in cui nessuno dei due prigionieri accusa l’altro (1,1) ed i due casi in cui solo A o solo B accusano l’altro (0,7 e 7,0). Se ci si trova nella situazione in cui entrambi accusano l’altro, infatti, è possibile ottenere un vantaggio per entrambi se tutti e due ritirano l’accusa.

 

 

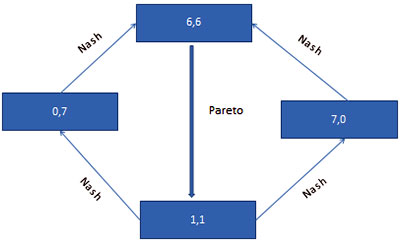
Nelle due situazioni intermedie, invece, se l’unico prigioniero che ha accusato l’altro ritirasse l’accusa avrebbe un danno, passando dalla libertà ad un anno di carcere. Anche questi sono quindi ‘ottimi di Pareto’ perché non è possibile migliorare la situazione dell’uno senza peggiorare quella dell’altro e rappresentano una allocazione ottimale delle risorse. Un ‘ottimo di Pareto’ non è però necessariamente la situazione migliore per la ‘società’.

 

L'allocazione ottimale

E’ evidente che la situazione migliore per la ‘società’ dei due prigionieri è quella in cui nessuno dei due parla, ma non ci si può arrivare in modo univoco con strategie egoistiche. E’ necessario un intervento esterno, ad esempio il capo della banda che è interessato ad avere a disposizione i due complici in uguale misura e che fa sapere ai due prigionieri che, se parlano, appena liberi gli verrà tagliata la testa.

Le strategie egoistiche non portano ad una soluzione ottimale per la società né se non ci si cura di quanto succede agli altri (come quando si calcola l’equilibrio di Nash) ma neppure se si è disposti a collaborare a patto di non avere svantaggi (come nella ricerca dell’ottimo di Pareto). E’ possibile che per ottenere la situazione migliore si debba imporre a qualcuno di rinunciare a qualche cosa: in una società evoluta questo è il ruolo della legge.

 

   Alberto Viotto

 

Se qualche lettore trovasse questo articolo interessante o ne volesse discutere, all'autore farebbe piacere ricevere delle e-mail all'indirizzo: alberto_viotto@hotmail.com

Altri articoli di Alberto Viotto

Guarda le novità del sito Sostieni Riflessioni.it sito web senza pubblicità
Seguici su Facebook	Seguici su Twitter
Libri pubblicati da Riflessioni.it 365 MOTIVI PER VIVERE Un motivo per ogni giorno dell'anno RIFLESSIONI SUL SENSO DELLA VITA 10 domande a 100 personaggi del mondo della cultura 1000 risposte a confronto