Menu principale
Menu

Mostra messaggi

Questa sezione ti permette di visualizzare tutti i messaggi inviati da questo utente. Nota: puoi vedere solo i messaggi inviati nelle aree dove hai l'accesso.

Mostra messaggi Menu

Messaggi - Eutidemo

Pagine 1 ... 81 82 83 84 85 ... 410
#1231
Varie / Re: Un enigma del finito.
25 Settembre 2023, 06:43:14 AM
Ciao a tutti gli intervenuti. :)
Le vostre considerazioni sono tutte interessantissime, in buona parte condivisibili e degne di pregio; però, per lo più, a me sembrano non rispondere direttamente al quesito iniziale di Iano: "Qual'è quell'insieme che è finito ma non limitato?"
L'unica risposta diretta a tale quesito, a me sembra che la fornisca solo Iano, quando scrive: "Io propongo l'insieme di tutti gli insiemi finiti pensati."; però, secondo me, alla stessa stregua si potrebbe proporre anche: "l'insieme di tutti gli insiemi limitati pensati".
Non vedo gran differenza!
***
Per quanto mi riguarda, ho già scritto che, almeno secondo l'accezione comune dei termini:
.
a)
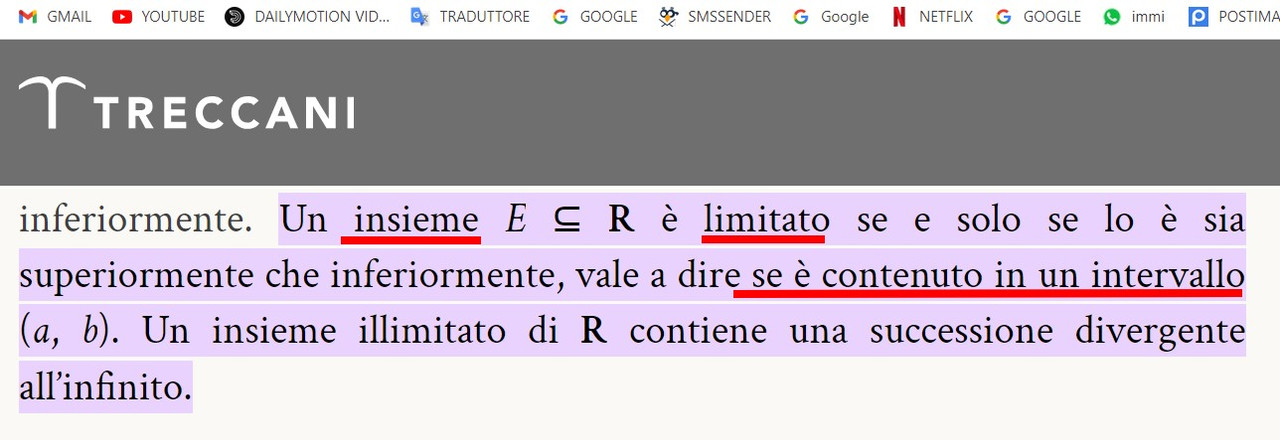
Un "insieme limitato", per definizione, deve avere necessariamente dei "limiti", cioè deve essere contenuto in dei "confini" ("limites") che lo delimitano; altrimenti sarebbe un "insieme illimitato".
.
b)
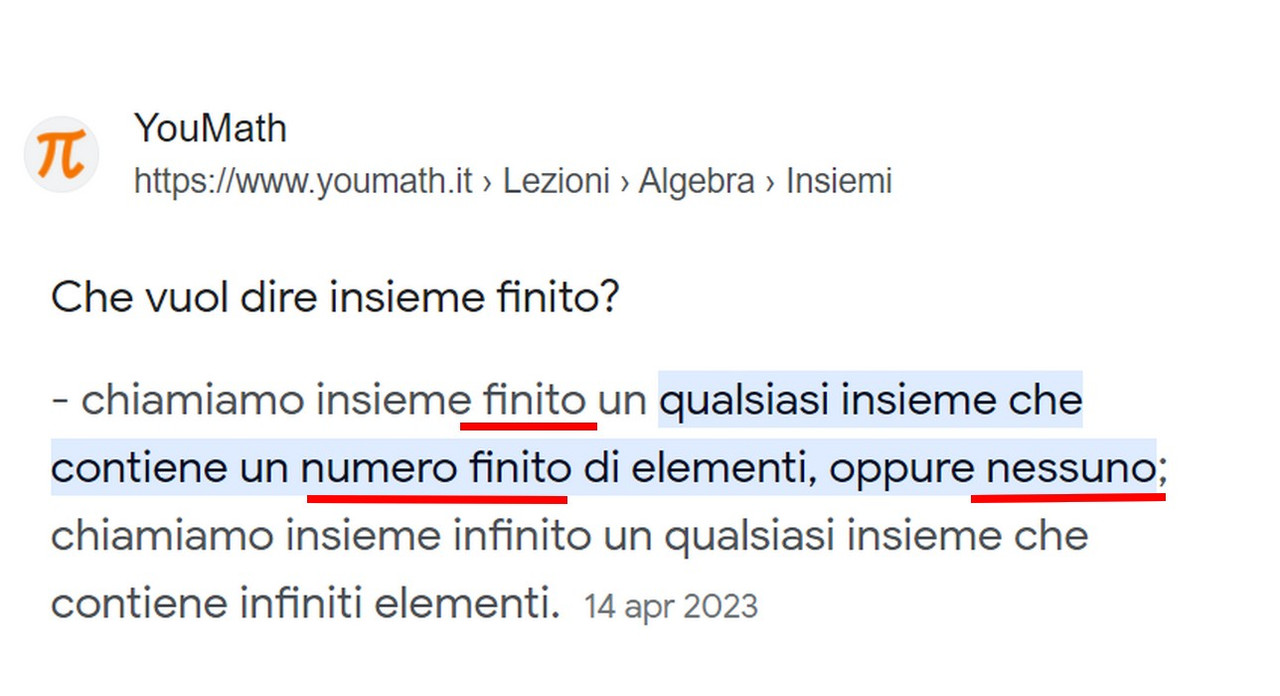
Un "insieme finito", invece, non comporta necessariamente l'esistenza di "limiti", ma, per definizione, deve contenere necessariamente:
- un numero finito di elementi;
- oppure nessuno.
***
Ora, il quesito iniziale era: "Qual'è quell'insieme che è finito ma non limitato?".
Per cui, a mio parere, secondo l'accezione comune dei termini, l'insieme che è "finito", ma non "limitato", è  "quell'insieme che non contiene nessun elemento"; ed infatti, in questo caso, non contenendo nessun elemento, non può aver dei "limiti", perchè non c'è niente da "delimitare".
***
,
***
Circa le critiche al mio ragionamento da parte di Iano, in sintesi:
a)
Se il "limite" fosse sempre concettualmente "valicabile", allora non potrebbe più concepirsi nessun "insieme limitato"; il che andrebbe contro i presupposti del quesito.
b)
Ogni "limite" può essere anche essere considerato come un "estremo", se gli elementi che compongono l'insieme vengono "elencati" e considerati in un determinato "ordine".
Ad esempio, noi Italiani viviamo "confinati" fisicamente e geograficamente dal mare e dalle Alpi; però,  in ordine alfabetico i limiti "estremi" sono costituiti da Abele Aab, e Zuzzurro Zuzzerelloni. ;D
***
.
***
Un cordiale saluto a tutti!
***
#1232
Varie / Re: Un enigma del finito.
24 Settembre 2023, 07:05:50 AM
Ciao Iano. :)
Al riguardo, secondo me, occorre previamente tenere conto della seguente differenza:
.
a) INSIEME LIMITATO
Un insieme si considera "limitato" se è contenuto tra due estremi che, appunto, lo limitano (da "limes" = "confine").
.
b) INSIEME FINITO
Un insieme si considera invece "finito", se contiene un numero finito di elementi; oppure non ne contiene nessuno.
***
.
***
Per cui, credo che un insieme "finito" ma "non limitato" sia un insieme "vuoto"!
***
.
***
Un cordiale saluto! :)
***
#1233
Tematiche Filosofiche / Re: Pensieri oziosi di un ozioso: 1 x 1 = 4
24 Settembre 2023, 06:47:11 AM
Ciao Knox :)
In ordine alle tue argomentazioni, osservo quanto segue:
1)
Tu scrivi: "Non bisogna confondere il metodo di formare un quadrato mediante l'accostamento di quattro segmenti, col quadrato ottenuto, nel quale i segmenti non ci sono più tranne che uno voglia estrapolarli, ma allora ci sarebbe un quadrato più quattro estrapolazioni, cioè delle figure sovrapposte!"
***
Trovo tale ragionamento del tutto "paralogistico", in quanto se tale argomentazione fosse logicamente valida, sarebbe valida, per assurdo, anche la seguente: ""Non bisogna confondere il metodo di formare un plotone mediante l'accostamento di trenta uomini, col plotone ottenuto, nel quale i soldati non ci sono più tranne che uno voglia estrapolarli, ma allora ci sarebbe un plotone più trenta estrapolazioni!"
***
In realtà, quindi, nel "quadrato" ottenuto, i "segmenti" ci sono ancora senza doverli "estrapolare", solo che si chiamano "lati"; così come i trenta "uomini" in divisa che formano un plotone si chiamano "soldati", ma non per questo cessano di essere anche degli "esseri umani".
***
Per cui, fuor di metafora, secondo me è errato sostenere che nel "quadrato" i "segmenti" non ci sono più tranne che uno voglia "estrapolarli", ne qual caso ci sarebbe un "quadrato" più "quattro estrapolazioni", cioè delle "figure sovrapposte".
Ed infatti i quattro "segmenti" chiamati "lati", non sono affatto delle "figure sovrapposte" al quadrato; bensì, al contrario, definendone la forma, ne fanno parte integrante, pur mantenendo la loro natura geometrica di "segmenti".
.
2)
Tu scrivi "In geometria dire lato non significa dire segmento"!
Ma, se è vero che "non ogni segmento costituisce un lato", però è senz'altro vero che "ogni lato è costituito da un segmento"; come, peraltro, precisato anche nel Dizionario Treccani.
***
.
***
Un cordiale saluto! :)
***
#1234
Tematiche Filosofiche / Re: Pensieri oziosi di un ozioso: 1 x 1 = 4
21 Settembre 2023, 06:38:50 AM
Ciao Iano. :)
Al posto di ''quadrato'' si può anche scrivere ''perimetro del quadrato'', ma le cose non cambiano; ed infatti è dal suo "perimetro", e, cioè, dalla sua "forma" che ti rendi conto di avere di fronte un ''quadrato'' e non un "cerchio".
***
Allo stesso modo, in effetti, quando guardi un'"automobile", in realtà tu stai vedendo soltanto la sua "carrozzeria", e non il suo "telaio"; ma è dalla "carrozzeria" che ti rendi conto di avere davanti una determinata '"automobile".
Però non dici certo "Ho visto la carrozzeria di una Panda", bensì, semplicemente "Ho visto una Panda"; sebbene è dalla forma (perimetro) della sua "carrozzeria" che l'hai riconosciuta.
***
Quattro rette parallele che si incrociano, a me danno più l'idea di una "croce" che non di un "quadrato"; però non c'è dubbio che i quattro "segmenti" uguali che scaturiscono dal loro "incrocio", danno senz'altro luogo ad un "quadrato".
***
Per cui, in questo caso, il "quadrato", costituito dai 4 "segmenti" uguali messi a ''quadrato'' all'incrocio delle parallele (detti "lati"), è proprio un povero "quadrato" messo  in "croce".   :D
***
.
***
Un cordiale saluto! :)
***
#1235
Tematiche Filosofiche / Re: Pensieri oziosi di un ozioso: 1 x 1 = 4
20 Settembre 2023, 13:02:04 PM
Ciao PhyroSphera. :)
Io non "presumo" affatto, bensì mi limito semplicemente a "constatare" che, in fin dei conti, un "quadrato" è costituito da quattro "segmenti"; i quali vengono da noi denominati "lati" solo per il fatto che sono disposti in un certo modo.
Ma sempre "segmenti" sono!
***
Con quattro "stuzzicadenti" o quattro "fiammiferi", a seconda del modo con cui li disponi, puoi ottenere sia un "quadrato" che una "croce"; nel primo caso li chiami "lati" del quadrato, nel secondo caso li chiami "bracci" della croce, ma sempre "stuzzicadenti" o "fiammiferi" restano.
***
E la stessa cosa vale per i "segmenti"!
***
Quanto al fatto che parlare di "segmenti" non sia una "descrizione" ma una "astrazione", in effetti anche le "astrazioni" sono suscettibili di" descrizioni"; nessuno ha mai messo in dubbio una cosa del genere!
***
Per cui non c'è dubbio che i "segmenti", in effetti, costituiscono davvero (come correttamente scrivi tu) dei "concetti astratti".
Ma non meno:
- del "perimetro";
- dell'"area.
I quali sono senz'altro anch'essi dei "concetti astratti".
***
Ed invero, il "perimetro" è composto da "quattro lati", i quali non sono altro che dei "segmenti" le cui estremità si toccano a 90 gradi; niente di più, e niente di meno!
***
La circostanza che il "perimetro" sia "continuo", non cambia assolutamente il fatto che esso sia la somma di quattro distinti "segmenti", chiamati "lati"; la diversità di nome dell'insieme, non cambia la denominazione degli elementi che costituiscono l'insieme (uno scheletro è fatto di ossa).
***
Quattro "segmenti" messi a forma di "quadrato" costituiscono senz'altro un vero "quadrato"; ed infatti, se io mettessi al posto di ogni "lato" una "semiretta" invece di un "segmento", non otterrei nulla che possa essere descritto come un "quadrato".
***
Cordiali saluti! :)
***
#1236
Tematiche Spirituali / Re: "Dio mio, Dio mio, perché mi hai abbandonato?"
19 Settembre 2023, 06:56:09 AM
Ciao  PhyroSphera.
Condivido, in buona parte, ciò che hai scritto; e, al riguardo, osservo quanto segue.
.
1)
Ritengo molto probabile che, in buona parte, quanto avvenuto durante la crocefissione, sia stato scritto  "a posteriori", per conferire valore profetico al salmo 22 (21).
***
Ad esempio, si notino le seguenti "coincidenze" tra i versi del salmo 22 (21) e quanto riportato in alcuni vangeli circa la crocefissione.
a)
"Dio mio, Dio mio, perché mi hai abbandonato?" (verso 1) che è quanto avrebbe detto Gesù secondo i vangeli di Marco e Matteo già ricordati; se lo ha veramente detto, insisto nel dire che, secondo me, la sua era una "citazione di tipo rabbinico", ma non escludo che tali parole gli siano state attribuite a posteriori.
b)
"Egli si affida al Signore, Lo liberi Lui dunque!" (verso 8 ), che è quanto avrebbe gridato beffardamente la folla sotto la  croce secondo il vangelo di Matteo (Mt 27 42)
c)
"Si spartiscono fra loro le mie vesti e tirano a sorte la mia tunica." (verso 18), che è quanto avrebbero fatto i soldati romani sotto la croce, secondo il vangelo di Giovanni (Gv 19 23-24) e di Matteo (Mt 27 35).
***
.
2)
Hai anche ragione nel dire che il cristianesimo non nacque, se non in parte, dal pensiero di Gesù, ma scaturì  principalmente  da come lo interpretò e lo diffuse tra i "gentili" Paolo di Tarso; che era di nascita un "cittadino romano", anche se di "origine ebraica".
In effetti Cristo, più che di "religione cristiana", era di "religione ebraica" (anche se alquanto eretica); ed infatti la sua predicazione era rivolta ai soli Ebrei.
***
Lo dice lui stesso nel Vangelo di Matteo: "Non sono stato mandato se non alle pecore perdute della casa d'Israele...Non è bene prendere il pane dei figli e gettarlo ai cani"Mt 15,21-28.
La traduzione "cagnolini" è stata fatta per edulcorare un po' il fatto che Gesù aveva sostanzialmente dato della "cagna" alla Cananea, in quanto non era di stirpe ebraica; anche se poi le guarì egualmente la figlia.
***
.
***
Un cordiale saluto! :)
***
#1237
Tematiche Spirituali / Re: "Dio mio, Dio mio, perché mi hai abbandonato?"
18 Settembre 2023, 12:24:30 PM
Ciao Bobmax. :)
Siamo tutti epifenomeni dell'ESSERE, per cui Cristo era "divino" esattamente come lo siamo noi; l'unica differenza tra noi e Gesù, è che in lui si è verificato quello che io chiamo un "corto circuito ontologico", e, cioè, una commistione "a corrente alternata" tra l'IO individuale ed il (D)IO universale (cioè, il SE').
Ma la divisione tra l'"esistere" come "fenomeno onda" ed l'"essere" come "noumeno mare", almeno a livello di "manifestazione", secondo me, "salvo eccezioni", permane invariata in tutti gli altri esseri viventi (animali compresi).
***
Quanto al "demone", se lo intendi in senso buono, come il "δαιμόν" dei greci, secondo me corrisponde più o meno all'"atman" vedanta; il quale, in sostanza è il "doppelganger" interiore e superiore del mio "io-jiva".
***
Al "demonio" nel senso di "diavolo", invece, non ci credo affatto; salvo ad intenderlo come "non essere".
Ma il "non essere" non è; quindi non c'è "niente" di cui preoccuparsi!
***
Un cordiale saluto! :)
***
#1238
Tematiche Spirituali / Re: "Dio mio, Dio mio, perché mi hai abbandonato?"
17 Settembre 2023, 12:47:27 PM
Ciao Bobmax. :)
Non c'è alcun dubbio che Gesù fosse un "uomo"; ma, poichè ogni uomo è un "epifenomeno dell'Essere", era senz'altro anche "Dio" (l'onda è senz'altro un'onda, ma è anche mare).
***
Al riguardo, secondo me, occorre ricordare che quando i Giudei accusano Gesù di bestemmia, poiché egli aveva dichiarato "Io e il Padre siamo uno" Gesù citò il Salmo 82:6,(Giovanni 10:25 –30 - 33); nel quale c'è scritto "siete tutti Dio", in quanto il termine "Elohîm", pur essendo grammaticalmente un plurale, in ebraico, non indica una pluralità di dei ma il Dio *UNICO* per eccellenza *_"Dio"_*.
Quindi siamo tutti DIO; ovvero, se preferisci, Dio è tutti noi!
***
D'altronde Gesù, in un altro punto del Vangelo di Giovanni, è ancora più chiaro, quando dice rivolgendosi ad una folla di esseri umani come noi: "Perché tutti siamo una sola cosa; come tu, Padre, sei in me e io in te, siano anch'essi in noi una cosa sola. E la gloria che tu hai dato a me, io l'ho data a loro, perché siano come noi una cosa sola. Io in loro e tu in me, perché siano perfetti nell'Unità" (Giovanni 17,21-23)
***
L'unica differenza tra Gesù e gli altri uomini, è che in lui si è verificato una sorta di "corto circuito ontologico", tra la sua "natura fenomenica individuale umana" (onda) e la sua la sua "natura noumenica universale divina" (mare); cosa che, per noi altri, sarebbe impensabile!
***
Circostanza, questa, notata anche da San Bernardo, quando scrive che Gesù, con terminologia moderna, era preda di una sorta di "schizofrenia ontologica"; in quanto a volte parlava come uomo, mentre altre volte parlava come Dio.
(BERNARDO DI CHIARAVALLE, "I gradi dell'umiltà e della superbia"10/11)
.
***
Un cordiale saluto! :)
***
#1239
Tematiche Spirituali / Re: "Dio mio, Dio mio, perché mi hai abbandonato?"
16 Settembre 2023, 11:36:34 AM
Ciao Bobmax. :)
In realtà, noi non sappiamo cosa "davvero" disse Gesù sulla croce, perchè Giovanni, che (forse) c'era, non riferisce affatto che il crocefisso pronunciò la frase ""Elì, Elì, lamà sabactáni?"; la quale frase è invece riferita soltanto da Matteo e da Marco, che sotto la croce non sembra affatto che ci fossero.
Sempre ammesso e non concesso che i due redattori degli omonimi vangeli fossero ebrei e avessero mai conosciuto di persona Cristo; e non si siano, invece, limitati a riportare (più o meno correttamente) quello a loro riferito (più o meno veritieramente) a voce da da Matteo e da Marco!
***
Per cui, vera o inventata che sia la citazione, insisto nel dire che è molto difficile che un "grido spontaneo" possa "casualmente" corrispondere "tel quel", parola per parola, ad un "verso dei Salmi".
***
Per cui insisto nel sostenere che, autentica o ricostruita a posteriori che fosse tale frase, chi l'ha riportata nei due Vangeli aveva ben chiaro che:
1)
Gesù era un "Rabbi", cioè un "maestro" delle scritture sacre.
2)
I "Rabbi" usavano sempre citare soltanto "i versi iniziali" di un salmo biblico per richiamarlo, però, nella sua "interezza".
3)
Costituisce, quindi, un gravissimo errore interpretare "i versi iniziali" di un salmo biblico citati da un Rabbi, soltanto nel loro specifico ed "autonomo" significato, senza considerare quello che dicono "i versi successivi" ed "esplicativi" dell'intero salmo.
Soprattutto quando "i versi iniziali" sono formulati come una "domanda" che attende una "risposta".
***
Se così non fosse, d'altronde, nè Marco nè Matteo (o chi per loro), si sarebbero mai sognati di riferire una mera "frase di disperazione" di Gesù fine a se stessa; ben sapendo che, invece, all'epoca tutti i giudei avrebbero ben compreso che in essa erano impliciti i versi successivi del Salmo 22 (21):""Tu mi hai risposto! Perché (Dio) non ha disprezzato né disdegnato l'afflizione del povero, il proprio volto non gli ha nascosto ma ha ascoltato il suo grido di aiuto."
***
Un saluto! :)
***
#1240
Tematiche Spirituali / Re: "Dio mio, Dio mio, perché mi hai abbandonato?"
15 Settembre 2023, 16:37:47 PM
Ciao Anthony. :)
Hai ragione, il salmo 22 (21) viene considerato "profetico"; sia nei passi che hai ricordato tu, sia anche in altri.
***
Ed infatti, ad esempio:
a)
Nel salmo 22 troviamo scritto:
"Si rivolga al Signore; lui lo liberi, lo porti in salvo, se davvero lo ama!" (versetti 9/10) .
b)
Nel vangelo secondo Matteo troviamo scritto che i capi dei sacerdoti, con gli scribi e gli anziani, facendosi beffe di lui sulla croce, dicevano: "Ha confidato in Dio; lo liberi lui, ora, se davvero lo ama." (versetto 43).
***
Un cordiale saluto! :)
***
#1241
Tematiche Spirituali / "Dio mio, Dio mio, perché mi hai abbandonato?"
15 Settembre 2023, 12:08:38 PM
Nei Vangeli di Matteo e di Marco, scritti in "greco", tale esclamazione viene "tradotta"  in modo univoco e corretto; sebbene la sua pronuncia venga riportata in maniera non del tutto identica dai due evangelisti.
***
A questo punto, però,  occorre chiarire alcuni punti, circa il "significato" di tale esclamazione di Gesù sulla croce; la quale, in genere, viene interpretata come un "momento di abbandono" e di comprensibile "angoscia".
***
Ed infatti:
1)
Gesù era un "Rabbi", cioè un "maestro" delle scritture sacre.
2)
I "Rabbi" usavano (e tutt'ora sovente usano) citare soltanto "i versi iniziali" di un salmo biblico per richiamarlo, però, nella sua "interezza".
3)
Costituisce, quindi, un gravissimo errore interpretare "i versi iniziali" di un salmo biblico citati da un Rabbi, soltanto nel loro specifico ed "autonomo" significato, senza considerare quello che dicono "i versi successivi" ed "esplicativi" dell'intero salmo.
Soprattutto quando "i versi iniziali" sono formulati come una "domanda" che attende una "risposta".
***
Ciò chiarito, almeno secondo me, le parole "Dio mio, Dio mio, perché mi hai abbandonato?", più che una "esclamazione fine a se stessa", vanno intese come una testuale "citazione rabbinica" di Gesù dei "versi iniziali" del salmo 22 (21); per cui è a quello, nel suo complesso, che Gesù intendeva riferirsi, e non ai singoli versetti iniziali considerati in modo indipendente!
***
Ed il significato complessivo del salmo 22 (21) costituisce una risposta ai suoi versetti di "abbrivio" formulati sotto forma di domanda!
Ed infatti, alla "domanda" formulata nei versetti iniziali "Dio mio, Dio mio, perché mi hai abbandonato?", più avanti, nello stesso salmo, leggiamo: "Tu mi hai risposto! Perché (Dio) non ha disprezzato né disdegnato l'afflizione del misero, il proprio volto non gli ha nascosto ma ha ascoltato il suo grido di aiuto."
***
#1242
Tematiche Filosofiche / Re: Pensieri oziosi di un ozioso: 1 x 1 = 4
14 Settembre 2023, 12:33:16 PM
Ciao Bobmax. :)
In effetti, anche se è vero che, nella maggior parte dei casi, la "moltiplicazione" non è altro che una "serie di addizioni",  tuttavia non sempre è così; ed infatti, come giustamente scrivi tu, dal "segmento" si giunge al "quadrato", per mezzo di una "moltiplicazione" (potenza), e non per mezzo di una  serie di "serie di addizioni" .
***
Il che, almeno in alcuni casi rende un po' "paradossale" il simbolo di "=" tra numeri, almeno all'apparenza "uguali", ma che, invece, non sono affatto  "uguali" (cifre a parte).
***
Ed infatti.
.
1)
Talvolta può accadere che:
a)
2 + 2 = 4
b)
2 x 2 = 4
c)
però 4a ≠ 4b
Ma 4 diverso da 4 non va contro il principio di identità?
NON SEMPRE!
***
Ed infatti può trattarsi di due "4" di diversa "natura geometrica":
- i primi 4 "metri lineari";
- i secondi 4, invece, "metri quadrati".
Per cui, nell'esempio di cui sopra, potremmo in un certo senso scrivere che 4 ≠ 4:
- se il primo 4 deriva dalla somma di 2 segmenti di 2 metri lineari ciascuno;
- se il secondo 4, invece, deriva  2 segmenti di 2 metri lineari moltiplicati per 2.
***
.
2)
Nel caso di 1, nello stesso caso, avremo invece due risultati già diversi di per sè in partenza:
Ed infatti:
a)
1 + 1 = 2
b)
1 x 1 =1
c)
2 ≠ 1
Il che è ovvio anche al semplice livello aritmetico, sebbene possa trattarsi non solo di una diseguaglianza di "quantità", bensì anche di una differenza di "natura geometrica"; ed infatti "2 metri lineari" non hanno niente a che vedere con "1 metro quadrato" (che di metri lineari ne ha ben 4 di perimetro).
***
.
***
Molto interessante il tuo riferimento alla "Critica della Ragion Pura" di Kant, laddove scrivi che il quadrato non è implicito nel segmento, per cui è un "giudizio sintetico a priori"; ciò  in quanto allarga la conoscenza in quanto è "sintetico", ma è anche universale e necessario in quanto "a priori".
***
Un cordiale saluto! :)
***
#1243
Tematiche Filosofiche / Re: Pensieri oziosi di un ozioso: 1 x 1 = 4
13 Settembre 2023, 11:34:31 AM
Ciao Iano. :)
Hai ragione: è un trucco semplice , che, però, illustra un concetto molto profondo.
E, cioè, che l'occhio (e il cervello), vedono solo quello che vogliono vedere; e, a volte, le persone mostrano agli altri  solo quello che loro desiderano vedere.
Come in campo finanziario, laddove, a volte, ti vogliono far credere che 0 x 0 = 50. :D
https://uploadnow.io/f/63TDVyB
Per non parlare della politica!
***
Un cordiale saluto! :)
***


#1244
Tematiche Filosofiche / Re: Pensieri oziosi di un ozioso: 1 x 1 = 4
13 Settembre 2023, 06:54:50 AM
Ciao Iano :)
Visto che tu mi hai chiamato il "Mago di Oz" perchè sono riuscito a fare "1 x 1 = 4" con i "segmenti",  per dartene ulteriore conferma, ho fatto "1 x 1 = 4" anche con le "monete"; il che è molto più redditizio. :D
Come si vede nel seguente videoclip:
https://uploadnow.io/f/kPxLtXp
***
Un cordiale saluto! :)
***
P.S.
E' un gioco di prestigio per "bambini"; per cui, visto quanto è semplice ed elementare, credo che non valga neanche la pena di stare a spiegarti qual'è il trucco. Ma, se serve e ti interessa, te lo spiego lo stesso, così potrai farlo ai tuoi nipotini! ;)
#1245
Tematiche Filosofiche / Re: Pensieri oziosi di un ozioso: 1 x 1 = 4
13 Settembre 2023, 06:26:01 AM
Ciao Iano. :)
Hai ragione!
Ed infatti:
- la MATEMATICA consiste nello studio delle misure e delle proprietà delle quantità, usando numeri e simboli.
- L'ARITMETICA, invece, è una branca della matematica che si occupa delle proprietà dei numeri.
***
Per il resto:
.
1)
A parte l'"1", tutti gli altri numeri sono soltanto degli "pseudonimi" abbreviativi delle addizioni del numero 1.
Ed infatti:
- "2" è il "nick name" di "1+1"
- "3" è il "nick name" di "1+1+1"
- "4" è il "nick name" di "1+1+1+1"
e così via per tutti gli altri numeri!
.
2)
Inoltre hai perfettamente ragione anche nel dire che le "moltiplicazioni" non sono altro che un "abbreviativo" delle "addizioni"; ed infatti si fa prima a scrivere 3 x 3 = 9, piuttosto che 3 + 3 +3 = 9.
Ma 1 x 1 non fa 2, come invece fa 1 + 1 = 2; per cui che senso ha?
Ha senso solo in geometria, per costruire un "metro quadrato"!
.
3)
Per cui condivido anche la tua morale della favola: "Attenti a introdurre semplificazioni che rendano più agevoli le nostre operazioni, perchè ciò mette alla nostra portata la capacità di complicarle ulteriormente, introducendo abbreviazioni di abbreviazioni che rischiano di assumere un significato indipendente da quello iniziale, per cui diventa impossibile ripercorrere il processo all'inverso al fine di comprenderne l'origine, ma è per via di questo paradosso , laddove la semplificazione complica, che si evolve la matematica e il linguaggio in generale introducendo per tale via nuovi significati."
***
Un cordiale saluto! :)
***
Pagine 1 ... 81 82 83 84 85 ... 410