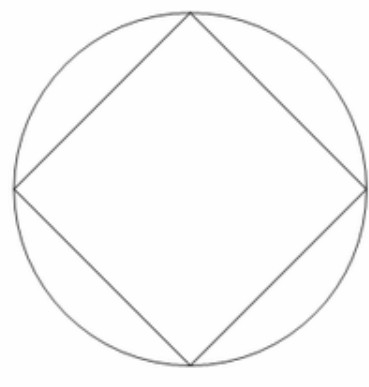
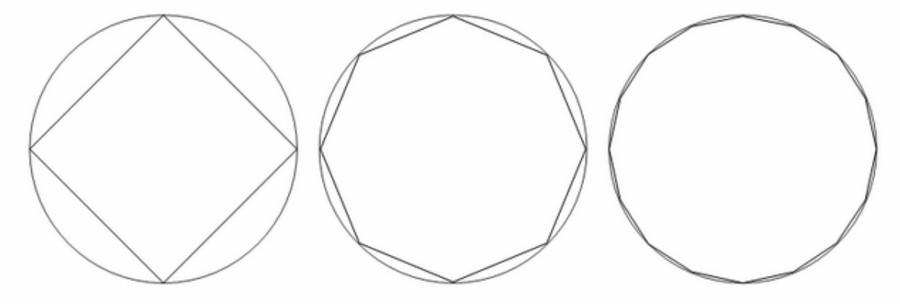
Citazione di: Eutidemo il 12 Giugno 2024, 17:22:20 PM

Così come mi ha fatto riflettere una interessantissima considerazione di BOBMAX, in risposta al mio enigma della "recinzione", il "poligono ciclico" è un "poligono" i cui vertici appartengono tutti ad una stessa "circonferenza".

***

Come, ad esempio, nel caso del seguente quadrato:

***

Ora, senza stare a calcolare le relative aree, salta all'occhio che l'area del cerchio che contiene il quadrato è senz'altro più grande dell'area del quadrato in esso contenuto: il che si desume anche in via meramente logica, perchè "il contenente è sempre maggiore del contenuto".

***

Salta anche all'occhio, d'altronde, senza stare a calcolare le relative aree, che la differenza di ampiezza tra l'area del cerchio che contiene un qualsiasi poligono e l'area del poligono in esso contenuto, diminuisce progressivamente con l'aumentare dei lati del poligono stesso.

***

Non saprei dire (senza fare dei calcoli) se la differenza di ampiezza tra l'area del cerchio che contiene il poligono e l'area del poligono in esso contenuto, diminuisca in modo "inversamente proporzionale" all'aumento dei lati del poligono stesso; però non c'è nessun dubbio che, con l'aumentare di tali lati, la differenza tra l'area del cerchio che contiene il poligono e l'area del poligono in esso contenuto diminuisce sicuramente sempre di più, tendendo all'"eguaglianza".

***

A questo punto, mi chiedo se sarebbe possibile definire il "cerchio" come un "poligono con un numero infinito di lati"; però, in tal caso, ogni lato dovrebbe avere una "lunghezza pari a 0" (zero).

***

P.S.

A questo punto, però, se non ricordo male:

- qualsiasi numero moltiplicato per zero, dà come risultato zero;

- qualsiasi numero moltiplicato per infinito, dà come risultato infinito.

***

Ma cosa succede se moltiplichiamo zero (che è un numero) per un numero infinito?

***

Non saprei proprio cosa rispondere!

E voi?

Infatti ogni lato del poligono non sarebbe zero, bensì un infinitesimo.

L'infinitesimo non è mai nullo. Non può proprio esserlo, perché se lo fosse non potrebbe essere utilizzato.
Lo si tratta così attraverso il differenziale. Che indica lo scostamento dell'infinitesimo rispetto allo zero.

Lo stesso dicasi reciprocamente per l'infinito. Il quale non esiste mai davvero. Perché anch'esso, se vero, non potrebbe essere utilizzato in alcun modo.

Di modo che l'infinitesimo è "quasi" zero e l'infinito è "quasi" davvero infinito.
In questo modo, con quel "quasi", li possiamo utilizzare. Così infinitesimo per infinito dà un valore finito.

Questa è la matematica e pure la filosofia.
Poi ognuna può andare dove meglio crede, ma le loro basi sono le medesime.

Ma la circonferenza non ha spessore.
Ce l'ha l'anello.
Un anello corrisponde a due cerchi concentrici.

Se invece nell'anello vi si vogliono vedere tutte le possibili circonferenze tracciatevi, queste sono infinite.

Citazione di: niko il 08 Giugno 2024, 22:51:27 PMCapisco cosa vuoi dire, ma per me il tempo e' circolare ed eternamente ritornante percio' l' "origine di tutte le cose" non esiste.

Ogni attimo, di questo cosmo che e' nel tempo, e' sia iniziale, che finale, che intermedio. Compreso questo attimo, nel qui ed ora.

Per me, la concezione lineare del tempo e' il piu' grande degli antropomorfismi: l'uomo, fenomenico ed esperibile, inizia e finisce, e immaggina, a vari livelli, un cosmo simile a lui, un cosmo che anch'esso inizi e finisca.

Ma io personalmente, rifiuto questo antropomorfismo. La natura, ha ben il diritto di differire da me. Nel suo non iniziare e non finire. Mentre io lo faccio.

Anche nel piu' rigido meccanicismo, il concetto di "caso" viene recuperato nel concetto di dipendenza, del sistema, dalle condizioni iniziali. Esistono le leggi di natura, ed esistono le condizioni iniziali, e, per prevedere cosa succedera' in ogni attimo, si deve avere contezza di entrambe.
Ma se ci spingiamo ancora piu' oltre nel meccanicismo, e immagginiamo un sistema locale, circolare e infinito, e ripetentesi all'infinito nel tempo, non esistono (piu') condizioni iniziali, per far rientrare dalla finestra il concetto di "caso". Le condizioni iniziali non ci sono, o meglio non hanno senso, sono qualsiasi momento e qualsiasi punto.

Rimane solo gelida necessita'.

E al limite volonta', vita.

Vita che presso la necessita' abita, e che in definitiva non puo' fare altro che abbracciarla, corrispondervi con un inane sforzo.

Sì, il divenire può essere inteso lineare oppure circolare.
Ed è quest'ultima interpretazione pure quella di Nietzsche.
Il divenire come ultima verità, cioè la Verità.

E per Nietzsche non poteva essere che così, volendo a tutti i costi rimanere fedele alla terra. Che poi in realtà era un voler rimanere fedeli alla propria interpretazione razionale della terra...
E così immagino fai tu.

Però in Nietzsche vi è pure tanta disperazione. Un dolore a cui reagisce sfidando lo stesso divenire, con l'oltreuomo.
Ma perché questa sofferenza?
Il motivo non è forse etico?
Un'etica che confligge con il divenire.

Prevale la certezza del divenire, della verità razionale, a scapito dell'etica.

Etica, che in Nietzsche è però fondamento di ogni suo agire.
Difatti lo stesso Nietzsche percepisce, qui e là, la possibile non verità del divenire. Ma non vuole ingannarsi!
Da onest'uomo che è.

Senza avvedersi che non si tratta di auto ingannarsi. Bensì di affrontare il nulla valoriale, implicito nel divenire, con il Nulla sostanziale!
Essere = Nulla

Solo così l'etica prende il sopravvento.

Dio = Caos

162,9088

Poligono ciclico 

Il perimetro quadrato, con lato di 250m, lo fa diventare circolare con raggio di 162m.

Citazione di: Koba II il 08 Giugno 2024, 11:31:40 AMSecondo me nel tuo ragionamento c'è un errore.
Tu dici: se la causalità è infranta allora entriamo nell'ambito del caos (della casualità), dopodiché mostri che le conseguenze di esso implicano la stessa conseguenza del dominio della necessità, ovvero l'impossibilità del libero arbitrio.

Noi però non abbiamo altro modo di comprendere la realtà che attraverso la causalità. Per cui se dovessimo trovarci di fronte ad una eccezione, allora tutta la nostra capacità di conoscere il mondo sarebbe confutata. Cioè avremmo per così dire la prova che conoscere per noi può significare solo tentare di interpretare la natura.
Cioè, mettere in crisi il nesso di causalità non ci condurrebbe a soppesare l'altro versante, quello del caso, quindi valutando le conseguenze filosofiche dell'esistenza reale di un fenomeno senza un perché, ma saremmo condotti invece a riflettere sui limiti delle nostre capacità conoscitive, e anche sulla consistenza ontologica dei concetti di causalità e di caso.

Non so se sono riuscito a spiegarmi...
Il tuo ragionamento è: se A (causalità) non è sempre vero, e quindi B (il caso) si manifesta, allora vediamo cosa ne consegue da B. E ciò che ne consegue è ancora la negazione di C (il libero arbitrio).
Ma se A non è sempre vero, allora la nostra stessa capacità di conoscere il mondo per quello che è viene meno, quindi non ha senso valutare B.
Piuttosto la conseguenza del fatto che A non è sempre vero è la dimostrazione che la nostra conoscenza non sa se le sue asserzioni hanno valenza ontologica: riducendo di necessità il sapere a qualcosa di strumentale.

Concordo con il tuo ragionamento.
E pure sono d'accordo che, nella tua prospettiva, nel mio discorso compaia un errore.
Infatti la tua considerazione è corretta, logicamente corretta.
E conduce in una situazione di stallo.

Inevitabilmente, perché per proseguire, il pensiero logico dovrebbe fare a meno di ciò che lo fonda.

Questa è la ragione per cui parlavo di un necessario cambio di prospettiva.
Cioè privilegiare l'etica alla logica.

Non per sbragarsi nel fantasticare illogico! Ma per giungere là dove la logica subisce lo smacco e provare a intuire se vi possa essere comunque una risposta.
Una possibilità inconcepibile logicamente, ma che sia comunque etica.

La butto lì, come possibilità paradossale (ma non troppo):

Se la necessità, cioè la legge di causa-effetto, non esistesse per niente?
Se nessun evento avesse mai una causa?

Se cioè il Caos fosse qui, ora, onnipresente?

Perché supporlo?

Etica.

Citazione di: niko il 08 Giugno 2024, 11:19:18 AMI sostenitori del libero arbitrio ti direbbero che no: oltre al caso e/o alla necessita', qualcosa, nel mondo avviene, pure per il libero arbitrio degli esseri viventi intelligenti.

In effetti il libero arbitrio e' un'origine degli eventi terza, rispetto sia al caso che alla necessita'.

Ed e' l'unica origine degli eventi che contempli la liberta'.

Infatti, se in ogni momento e in ogni aspetto della mia vita io fossi in balia del caso, e/o della necessita', non sarei libero.

Io comunque, contemplo e ammetto solo la necessita'.

Non c'e' alcun caso e, ovviamente non c'e' alcun libero arbitrio, in niente, di reale.

Posizione netta e senz'altro legittima, quella di escludere il caso in quanto non reale.
E direi pure doverosa, il caso non esiste. Non può esistere.

Tuttavia, anche se lo escludi qui, nel presente, non ricompare forse alla origine di tutte le cose?
Non sei forse qui, ora, per caso?

Ma se all'origine non può che esservi il caso, tutta questa onnipresente necessità, non è in fin dei conti essa stessa espressione del Caos?

Di modo che, non sei forse tu figlio del Caos?

Citazione di: Koba II il 08 Giugno 2024, 08:14:06 AMDue cose ci appaiono come evidenti:
1) essere liberi;
2) poter conoscere il mondo per come realmente è.

Domanda: perché la natura ci avrebbe dovuto ingannare sulla prima evidenza e non sulla seconda?
Entrambe queste due evidenze se sottoposte ad attenta analisi mostrano di essere problematiche.
E l'una esclude l'altra.

Probabilmente, per non dire certamente, sono vere entrambe.

Intendendo con "vere" la Verità.

Occorre però cambiare prospettiva. Cioè privilegiare l'etica rispetto alla logica.
Senza con questo accettare come logico ciò che è illogico. Ma andare invece oltre la stessa logica. Là dove la logica non può arrivare.

Tenendo allora ferma la libertà e la realtà, cosa succede al libero arbitrio individuale?

Perde quel "individuale".

"La divinità è nascosta, ma non maliziosa"

Citazione di: niko il 07 Giugno 2024, 15:47:34 PMCerto, che il libero arbitrio si oppone alla necessita'.

A che cosa senno'?

Il libero arbitrio individuale richiede che l'individuo, quell'individuo lì specifico, oggettivo, distinto da tutto il resto del mondo, sia: una origine incondizionata di eventi.

Ma la Necessità nega che vi possa essere qualcosa che sia davvero incondizionato.
Quindi la Necessità nega il libero arbitrio individuale.

Tuttavia, anche supponendo che la Necessità non sia onnipresente, che cioè la legge di causa-effetto possa essere infranta, ciò può avvenire soltanto ammettendo la realtà del Caso.
Giacchè ciò che avviene può avvenire soltanto o per Necessità o per Caso.

Ma il Caso, una volta reale, cosa implica?
Non nega forse anch'esso che possa esistere una origine incondizionata di eventi?
Infatti il Caso ammette l'incondizionatezza, ma nega che vi possa essere una origine!

La Necessità non permette l'incondizionato, il Caso annulla l'origine.

In nessun modo il libero arbitrio individuale è possibile.

Vorrei sottolineare: individuale...

Per dare un'idea di cosa significherebbe supporre il verificarsi di un evento, che non era necessario avvenisse, vorrei fare alcuni esempi:

Cade una mela dall'albero, senza che vi siano cause che l'hanno fatta necessariamente cadere.
La caduta della mela è avvenuta senza motivo...
Avrebbe potuto non cadere e invece è caduta, ma avrebbe potuto benissimo non cadere, visto che niente ha determinato la sua caduta.

Ho davanti un morto. Che è morto senza che vi siano cause sufficienti della sua morte, avrebbe potuto non morire.
E invece è morto.
Senza un perché.

Nasce un pensiero nella mente, avrebbe potuto non comparire, invece è comparso, senza motivo.

Dovrebbe essere evidente l'assurdità di queste situazioni prospettate, e quindi la loro impossibilità.
Se viceversa si insiste nel considerarle possibili, allora si nega il Cosmo e si afferma... boh, chissà, l'irrazionale?

PS
Non è la onnipresenza della Necessità a determinare la non esistenza del libero arbitrio.
Infatti il libero arbitrio individuale non esiste a prescindere dalla stessa Necessità.

La nostra realtà è il Cosmo.
E nel Cosmo regna la Necessità.
Essendo il Cosmo il luogo della esistenza, la stessa esistenza è scandita dalla Necessità.
Tutto ciò che esiste, esiste necessariamente.
Cose, eventi, pensieri, esistono in quanto necessari, tutto quello che c'è, c'è necessariamente.

Ci si potrebbe domandare per quale motivo si debba tenere ferma la onnipresenza della Necessità...
Perché tutto deve essere necessario?
Non potrebbe qualcosa non esserlo?

Per rendersi conto che non può esservi niente che non sia necessario, si dovrebbe supporlo invece esistente, valutandone le implicazioni...

Valutarle davvero però!
Non tanto per dire, come è solito fare il non pensiero.
Cosa significherebbe la esistenza di un qualcosa, di un fatto, che tuttavia non era necessario esistesse?

Come interpretare questa rottura della legge di causa-effetto?

Beh, semplicemente non si potrebbe interpretare in nessun modo. Sarebbe un puro non senso.
Ci troveremmo davanti l'assolutamente inconoscibile!
L'abisso della follia si spalancherebbe, perché il pensiero stesso si troverebbe di fronte (esistente!) ciò che lo trascende totalmente.
Saremmo un balía del Caos, che irrompe nel Cosmo quando gli aggrada!
La nostra esistenza sarebbe soltanto una colossale presa in giro...
Perché nulla potremmo mai davvero capire.

Per pensare qualcosa, infatti, è indispensabile darne per scontata la necessità.
Se non lo si fa, se si pretende che la necessità sia soltanto una possibilità, semplicemente non si sta pensando.

Di modo che anche solo per pensare, si deve dare per scontata la Necessità.

Ma se questo mondo, questo Cosmo necessario, non mi va bene?
Se l'esistenza così com'è non è accettabile, perché vi è il male?

E non posso rifugiarmi, nel non pensiero del voler credere che la Necessità possa essere qualche volta infranta? Proprio perché mi auto ingannerei, cadendo in superstizione?

Cosa mi resta?
A chi appellarmi?

Al Caos.
A Dio.

Nel Cosmo regna la Necessità.
Tutto nel Cosmo sottostà alla legge di causa-effetto. Perché non avviene nulla che non fosse necessario avvenisse.

A prescindere se determinabile o meno, ogni evento nel Cosmo avviene necessariamente.

Questo bisogna tenerlo ben fermo!
Perché supporre che possa avvenire qualcosa che non era necessario avvenisse, ci fa cadere nel vuoto.
Ossia nel credere la realtà di fenomeni irrazionali.

Il Cosmo occorre accettarlo come un tutto razionale e necessario.
O tutto o niente.

Difatti, se viceversa, magari per motivi etici, lo si vuole mettere in discussione. Allora il Cosmo lo si deve ipotizzare non vero nella sua interezza!
Supponendo la verità del Caos.

Citazione di: sapa il 05 Giugno 2024, 10:17:34 AMConcordo con Ipazia, di taurus leggo sempre tutto avidamente. L'ultimo post sui messia coevi del Nostro è stato per me una chicca. Purtroppo, non ho mai tempo di verificare le fonti che lui indica sempre, ma non ho ragione di pensare che non siano corrette. Anticlericalismo da osteria non direi proprio.

Penso non vi possano essere dubbi riguardo alla erudizione di Taurus.
E neppure che vi siano forti, legittime motivazioni per la sua ostilità verso il clero.

Tuttavia, la pur giusta reazione ai torti subiti finisce per tracimare in un ateismo rabbioso. Che rigetta non solo il dogma, che in quanto tale è sempre truffaldino, ma lo stesso Spirito.

Una reazione esagerata, ma peculiare in quelli che si sono staccati risentiti dalla Chiesa.
In quanto ingannati e usati da una congrega di pifferai magici.

Si finisce però così con il buttare il bambino con l'acqua sporca. E la responsabilità di tanta devastazione è tutta nella intrinseca ipocrisia e malvagità delle istituzioni religiose.

Ma il "capire" non è forse il risultato della elaborazione di una informazione?
E questo risultato non consiste in sostanza nell'accordo o non accordo di questa informazione con altre informazioni?

Viceversa il "sentire" appare più problematico.
Potrebbe essere nient'altro che un "capire" della cui elaborazione si è inconsapevoli.
Potrebbe essere dovuto all'istinto, che non è che il consolidamento di tante elaborazioni razionali (capire) passate e ormai automatizzate.
E così potrebbe essere l'intuito.

Ma il "sentire" potrebbe essere invece altro, radicalmente altro...
Ma di cosa si tratterebbe?

Secondo me, mentre il "capire" , in tutte le sue forme anche intuitive, riguarda l'esistere, vi potrebbe essere pure un autentico "sentire", che prescinde dal "capire".
Questo autentico "sentire" riguarda invece l'Essere.
Che è origine dell'esistere, ma a sua volta non esiste.

E che cos'è che si sente?
Il bene e il male.
Che prescindono dal capire.

Il sentire è sentimento dell'Essere.
È desiderio del Bene.
È il figlio che vuole tornare al Padre.

In questi ultimi tempi, al diffuso chiacchiericcio si è aggiunto un fenomeno a mio parere ancor più pernicioso.
Mi riferisco alla pubblicazione di testi, a firma di utenti, che in realtà sono stati molto probabilmente generati con l'IA.

Questo fastidioso sospetto nasce dalla osservazione di anomalie, altrimenti inspiegabili, come:

La forma espositiva ricalca quella di ChatGPT.
Le competenze del medesimo autore sembrano coprire tutto lo scibile umano.
Autore che non di rado cade rovinosamente, sia nella forma sia nella sostanza, con interventi grossolani, che stridono con la qualità e profondità espressa altrove: qui non è stata usata l'IA?

Una perplessità che può minare ogni fiducia nella controparte: ha ancora senso comunicare?