Menu principale
Menu

Mostra messaggi

Questa sezione ti permette di visualizzare tutti i messaggi inviati da questo utente. Nota: puoi vedere solo i messaggi inviati nelle aree dove hai l'accesso.

Mostra messaggi Menu

Messaggi - Eutidemo

Pagine 1 ... 123 124 125 126 127 ... 410
#1861
Tematiche Culturali e Sociali / Attenti ai "sosia" telefonici
17 Marzo 2023, 12:14:09 PM
Normalmente, io, per prudenza, non rispondo mai ai numeri ai quali non corrisponde nessun "nominativo" da me registrato nella "rubrica"; ma, ormai, sembra che i truffatori telefonici siano riusciti ad aggirare anche questo tipo di elementare cautela.
Vediamo come.
***
Truffe del genere, infatti, risultano attuabili grazie:
- ad operatori telefonici VOIP in territorio straniero (in genere russo) che danno questa capacità ai loro fraudolenti clienti in tutto il mondo;
- ad un sistema di inoltro delle telefonate, che lascia transitare sul proprio circuito comunicazioni provenienti da numeri già registrati sul suolo nazionale.
***
Per cui è naturale che le vittime cadano nel tranello; ed infatti, quello che vedono associato sia agli SMS, sia alle telefonate è il numero salvato in rubrica (per cui il trucco dovrebbe funzionare anche per WHATSAPP, ma di questo non sono sicuro).
***
Ed infatti la tecnologia VOIP (Voice Over IP) consente di impostare un "caller ID" (identificativo chiamante) "simulato", ed alcuni fornitori di servizi offrono di default tale possibilità; solo alcuni dei quali sono legali.
Come, ad esempio, lo è il tedesco "fakemyphone.it", il quale si può utilizzare per fare degli scherzi agli amici; però memorizza  tutte le attività degli utenti in modo da poter rispondere ad eventuali verifiche da parte della autorità giudiziaria.
Però molti altri fornitori di servizi, per lo più illegali, consentono l'assoluta anonimità ai loro clienti.
***
Inoltre, LYREBIRD, ha trovato il modo di riprodurre le caratteristiche vocali di qualsiasi persona con l'analisi di un solo minuto di parlato; per cui, "teoricamente", potreste veder apparire sul cellulare il nominativo di vostro cugino che vi chiama,  e, poi, sentire addirittura l'imitazione della sua voce.  
***
L'unico modo per proteggersi, quindi, soprattutto nel caso delle "banche", è di non fare troppo affidamento sul "caller ID" che viene esposto al momento della ricezione della chiamata; nella maggior parte dei casi certamente corrisponderà al "reale mittente" della chiamata ma esiste comunque l'eventualità che possa essere stato fraudolentemente simulato.
***
Ed infatti, ecco l'email che ho ricevuto oggi dalla mia banca:
***
#1862
Varie / Re: L'enigma dei collegamenti
17 Marzo 2023, 05:38:40 AM
Ciao Bobmax e Phil.
Come giustamente avete osservato entrambi (e come sapevo anch'io) senza utilizzare la "terza dimensione", collegare "contemporaneamente" i tre punti A, B, C ai tre punti  D, E e F senza mai intersecare o sovrapporre le varie linee è davvero "impossibile"; però non bisogna dimenticare che esiste anche una "quarta dimensione", la quale non è stata espressamente esclusa dalle regole del gioco, e quindi, secondo me, può benissimo essere utilizzata, rendendo senz'altro "possibile" realizzare i collegamenti in questione.
Il TEMPO! ;)
Utilizzando tale "quarta dimensione", infatti, diventa possibilissimo collegare i tre punti A, B, C ciascuno ai tre punti  D, E e F senza mai far intersecare o sovrapporre le varie linee; e, questo, anche in uno spazio assolutamente piano.
Come dimostrato dal seguente videoclip da me realizzato:
https://dai.ly/k65H1SVR5F4FAcyUpPN
 :D :D :D :D :D :D :D :D :D :D :D
***
Un saluto ad entrambi! :)
***

#1863
Varie / Re: L'enigma dei collegamenti
17 Marzo 2023, 05:23:07 AM
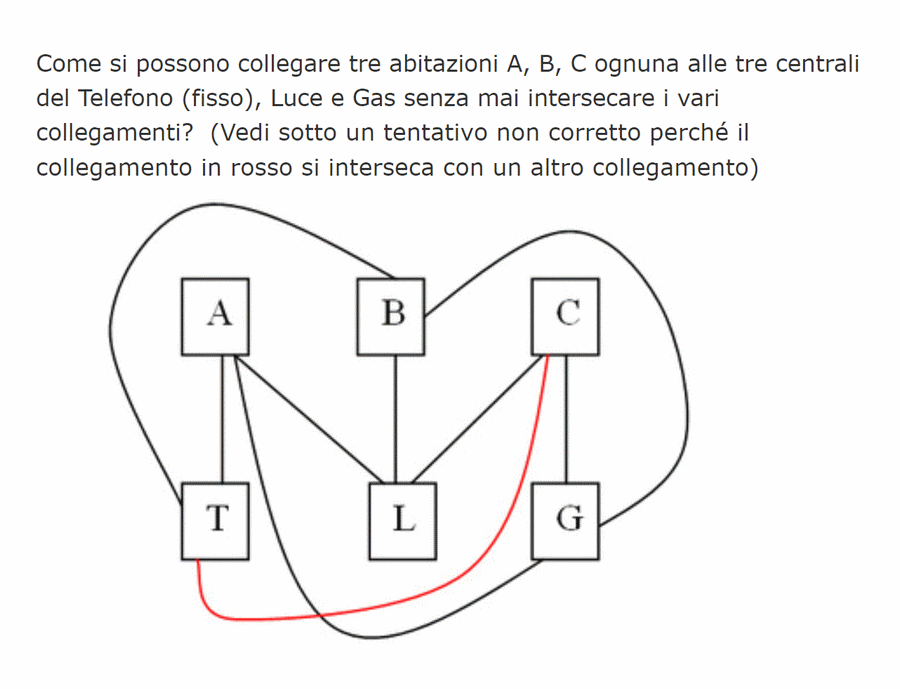
Citazione di: Phil il 16 Marzo 2023, 17:16:00 PMFacendo il "finto tonto", proporrei questa soluzione (anche se in realtà so che, una volta esplicitate tutte le regole previste dal "gioco", che già conoscevo, è impossibile fare tutti i collegamenti):

Interessante soluzione, sebbene una volta esplicitate tutte le regole previste dal "gioco" sembra davvero  impossibile fare tutti i collegamenti; ed infatti le linee non vanno nè "intersecate", nè "sovrapposte".
Non devono, cioè, avere nessun contatto tra di loro.
#1864
Varie / Re: L'enigma dei collegamenti
16 Marzo 2023, 16:44:50 PM
Citazione di: bobmax il 16 Marzo 2023, 13:26:13 PMÈ impossibile perché è un grafo non planare.
(Teorema di Kuratowski: è un grafo bipartito completo K3,3)
Dipende! :)
Un modo c'è, come mi riservo di dimostrare dopo altri eventuali interventi ;)
#1865
Tematiche Culturali e Sociali / Re: La "Roulette" e i "presunti" sistemi per vincere
16 Marzo 2023, 11:21:04 AM
Citazione di: Freedom il 12 Marzo 2023, 19:29:48 PMEutidemo, non posso contestare la incontrovertibile e matematica (statistica) veridicità delle tue affermazioni.

Però, non so per quale imperscrutabile e pervicacia testardaggine :)) , se siamo al tavolo della Roulette ed è uscito 7 volte il nero io punto il rosso.  8) :D Tu?
Pure io :D
#1866
Tematiche Culturali e Sociali / L'"Ouroboro" e il "Nastro di Moebius"
16 Marzo 2023, 11:00:13 AM
Il nome del serpente "Ouroboro" deriva dal greco "οὐροβόρος" ("οὐρά"  "coda," e "βορός", "mordente"); ma si trova scritto anche "Oroboro", "Uroburo" o "Uroboro" ecc., le quali sono tutte forme etimologicamente devianti, ma comunemente usate ed accettate.
***
Si tratta di un simbolo molto antico che rappresenta un "serpente che si morde la coda"; però, nei bassorilevi, viene raffigurato in due posizioni completamente diverse.
- a forma di "cerchio":
- a forma di "otto":
***
Oltre a tale evidente differenza, ho notato che, sebbene ci sia una infinità di diverse raffigurazioni delle due immagini, sia in quella a forma di "cerchio", sia in quella a forma di "otto":
- in alcune delle prime (cerchio) il serpente "inghiotte" la sua coda (cioè, se stesso);
- in alcune delle seconde (otto), invece il serpente "morde" soltanto la sua coda, senza "autodivorarsi".
Vedi, ad esempio, le immagini sopra.
***
Inoltre, sebbene in casi molto più rari di rilievi sepolcrali, il serpente a forma di otto la sua coda non la "morde" nemmeno, ma si limita semplicemente a "strisciare su se stesso".
***
Sulla base di tali estemporanee osservazioni, ho ritenuto di poter fare un'"ipotesi"; la quale, però, è estramemente "congetturale", e, secondo me, ha solo "una probabilità su dieci" di essere fondata (se non ancora di meno).
***
Al riguardo, si tengano presenti le seguenti considerazioni:
a)
Un serpente che "inghiotte" se stesso, paradossalmente "consuma" un cerchio annullandosi per sempre.
b)
Un serpente che "morde" se stesso (ovvero che striscia su se stesso), invece, paradossalmente, può continuare a farlo all'infinito.
***
Riguardo alla considerazione di cui alla lett.b), peraltro, si tenga presente che la maggior parte dei serpenti, hanno il "dorso scuro" e il ventre più "chiaro"; come quello nella seguente immagine.
***
Il che significa che se i serpenti si intorcinano su se stessi, a forma di otto (soprattutto morendo), assumono un aspetto molto simile all'"Otto di Moebius"; con un lato più scuro ed uno più chiaro.
I quali lati, però, sono uno la continuazione dell'altro, se il serpente si morde la coda ruotando la testa nello spasmo della morte; come talvolta accade.
***
Perciò non si può escludere che qualche antico filosofo greco, il cui nome è rimasto sconosciuto, abbia anticipato di secoli l'idea del "Nastro di Moebius"; identificando il serpente morto in posizione di otto all'"infinito percorso" che, su di esso, le formiche continuavano a fare, fino a ridurlo uno scheletro.
.
***
Non a caso l'attuale "Simbolo matematico dell'infinito", è molto simile sia ad un ad "Ouroboro" a forma di 8, che ad un "Nastro di Moebius" (e non ad un  "Ouroboro" a forma di cerchio)
***
Come ho detto, la mia è solo una fantasiosissima "congettura" (o, se preferite, una semplice "fantasia"); però, quantomeno sul piano filosofico, secondo me si può benissimo intravedere un "fil rouge" tra i tre diversi simboli (sebbene il "Nastro di Moebius" non sia soltanto un simbolo).
***
#1867
Percorsi ed Esperienze / Re: Il mistero del gatto!
16 Marzo 2023, 10:42:28 AM
Possibile che nessuno abbia notato che la sera prima il gattino ha la testa girata verso "destra", mentre, la mattina dopo, ce l'ha girata verso "sinistra"?
Voi come ve lo spiegate?
Come un augurio per le prossime elezioni? :)
#1868
Varie / L'enigma dei collegamenti
15 Marzo 2023, 11:53:23 AM
Su INTERNET ho trovato il seguente enigma: "Come si possono collegare le tre abitazioni A, B, C ognuna alle tre centrali del Telefono T, Luce L e Gas G senza mai intersecare i vari collegamenti?"
.
***
Al riguardo, secondo me, occorre distinguere i diversi aspetti del problema, sia sotto il profilo "concreto" che sotto quello "astratto":
.
1)
CONCRETAMENTE
Nella realtà fisica i collegamenti alle centrali del Telefono, Luce, e Gas  non si intersecano mai, perchè i cavi vengono impiantati, sottoterra, a diversi livelli di profondità; per cui l'enigma proposto non si pone materialmente in alcun modo. ;)
.
2)
ASTRATTAMENTE
Astrattamente, invece, con riferimento ai 6 punti A B C da collegare ciascuno ai punti D E F con linee (rette o curve) il problema si può porre in due modi diversi:
.
a)
Utilizzando la terza dimensione, si possono facilmente collegare i tre punti A, B, C ognuno ai tre punti  D, E e F senza mai intersecare nello spazio le varie linee;  il che è geometricamente facilissimo, come evidenziato dal seguente disegno.

.
b)
Però, senza utilizzare la terza dimensione, collegare su un piano i tre punti A, B, C ognuno ai tre punti  D, E e F senza mai intersecare le varie linee diventa un po' più difficile; così come evidenziato dal seguente disegno.
***
E' possibile o impossibile?
Voi cosa ne dite?
***
#1869
Percorsi ed Esperienze / Re: Il rebus del "parquet"!
14 Marzo 2023, 18:28:52 PM
Ciao Iano :)
 Su una cosa Bobmax ha pienamente ragione: io sono troppo "ridondante"!
Ed infatti esprimendo il mio ragionamento in modo molto più sintetico, e in parole molto più povere, una volta che io, tu e Bobmax abbiamo accertato (giustamente) che il lato di una mattonella è lungo 12 cm, perchè mai metterlo al quadrato e poi dividere il risultato per cinque, quando, per ottenere l'area del tassello è sufficiente moltiplicare direttamente  12 cm per 2,4 cm?
Non è più semplice?
Ed infatti il lato di una mattonella è lungo 12 cm esattamente come lo è  il "lato lungo" del tassello; e, visto che  il "lato corto" del tassello è necessariamente lungo 2,4 cm (perchè il "semiperimetro" del tassello è  28,8/2 =  14,4cm), la sua area si può ottenere con "un solo semplice calcolo mentale", moltiplicando 12 cm per 2,4 cm = 28.8 cmq
O forse sbaglio in qualcosa, visto che ora sono al letto con la febbre e senza calcolatrice? :(
***
Buonanotte! :) :) :)
***
#1870
Percorsi ed Esperienze / Re: Il rebus del "parquet"!
14 Marzo 2023, 17:12:44 PM
Ciao Iano.
Condivido completamente tutto quello che hai scritto!
Ed infatti io non ho mai gareggiato a chi avesse il ''segmento'' matematico più "lungo" (o meglio, in questo caso, più "corto"), riconoscendo immediatamente che sia il ragionamento tuo sia quello di Bobmax erano  assolutamente perspicui e corretti; ed infatti entrambi conducevano alla soluzione giusta. :)
Inoltre, ho più volte ripetuto (perchè è vero) che in matematica tu e Bobmax siete molto più competenti di me (e forse non solo il quella).
***
Però, mentre tu hai riconosciuto che anche il mio ragionamento era corretto, conducendo alla stessa giusta conclusione a cui era pervenuto il vostro, Bobmax ha cominciato a fare delle "considerazioni", alcune delle quali le trovo veramente assurde, o, quantomeno, molto bizzarre; per questo ci siamo messi un po' a "battibeccare"!
Non metto comunque minimamente in dubbio nè la sua intelligenza nè la sua competenza matematica, che è sicuramente superiore alla mia!
***
Quanto alle equazioni, riflettendoci, mi sono reso conto proprio adesso che (a parte quella di Bobmax, che è "correttissima" ma si ferma a metà strada dando per scontato il resto), le nostre due equazioni, almeno fino ad un certo punto, sono molto simili.
Ed infatti:
.
a) TUA EQUAZIONE
2(L + L/5) = 28,8 cm
Dove L è il lato del quadrato formato da 5 tasselli.
Si ricava L = 12 cm
L'area del tassello quindi è  (L quadro) / 5 = 28,8 cmq
.
b) MIA EQUAZIONE
2(L + L/5) = 28,8 cm
Dove, però, secondo il mio procedimento L  è considerato il "lato lungo del tassello", formato da 5 tasselli corti (ed anche se è un lato del quadrato formato da 5 tasselli, questo non interessa il mio procedimento).
Ed infatti L, il "lato lungo del tassello" CD,  sommato ad L/5, cioè DE, che è il "lato corto" del tassello, corrispondono esattamente al "semiperimetro" del tassello stesso preso in considerazione CDE, il quale non può essere lungo che 14,4 cm (28,8/2); dal che si deduce che il "lato lungo" del tassello CD, composto da cinque lati corti, deve per forza essere di 12,00 cm, mentre il "lato corto" DE = BD del tassello deve per forza essere di 2,4 cm,  (vedi mia immagine sotto).
Per cui si ricava non solo che L = 12 cm, come nella tua equazione, ma anche che L/5 = 2,4 cm; cioè la "base" e l'"altezza" del singolo tassello, a seconda della posizione che preferisci dargli.
***
A questo punto, i nostri calcoli finali, legittimamente, divergono, perchè:
.
a)
Tu (giustamente) calcoli l'area del tassello moltiplicando lato per lato la mattonella, e poi dividendo il risultato per 5
(L x L) = AREA MATTONELLA : 5 = AREA TASSELLO
12 x 12 = 144 cmq e poi 144 : 5 = 28,8 cmq.
.
b)
Io, invece, mi limito a moltiplicare tra di loro base per altezza L x L/5 = AREA TASSELLO
12 x 2,4 = 28,8 cmq
.
***
Tutto sommato, non per "fare a gara" a chi ce l'ha più lungo, bensì soltanto "pour parler" facendo entrare nell'equazione il "semiperimetro", a me "sembra" che il calcolo dell'area del tassello sia:
- più diretto;
- più corto;
- più semplice.
Ma forse sarebbe più esatto dire che vostre formule sono un po' più corte delle mie, ma i calcoli da fare sono un po' più lunghi e con cifre da moltiplicare e dividere più elevate.
***
Ma forse mi sbaglio!
***
In ogni caso, non c'è dubbio, almeno secondo me, che tutte e due le nostre procedure di calcolo siano perfettamente correte; altrimenti non perverremmo allo stesso identico risultato. ;)
***
Non ci vedo nessuna babele!
***
Un saluto!
***
P.S.
La mia equazione, in altra forma e con altri simboli, l'avevo già esposta nel seguente più dettagliato modo; ma la sostanza è identica a quella sopra.
La ripeto solo per ulteriore chiarezza.
------------------------------------------------------
Data X come incognita da trovare, e, cioè,  l'"area del tassello" (da cui poi ricavare, per moltiplicazione, sia quella di una singola mattonella, sia quella  di tutte e nove le mattonelle);
Dato P, come perimetro noto del tassello;
Dati come identici tutti i tasselli;
Dato LC come lato corto del tassello;
Dato LL come lato lungo del tassello;
Avremo:
P/2/6 = LC (2,4 cm)
LC x 5 = LL  (12 cm)
LC x LL = X (, cioè,  l'"area del tassello")
***
#1871
Percorsi ed Esperienze / Re: Il rebus del "parquet"!
14 Marzo 2023, 12:59:53 PM
Ciao Iano. :)
Non so come tu abbia interpretato il mio passo, ma io intendevo semplicemente dire che a me non risultava affatto l'esistenza una formula matematica che ci potesse fornire  direttamente l'area di un rettangolo, conoscendone soltanto il perimetro; però, considerata la mia ignoranza "geometrico-matematica", avevo soltanto aggiunto che, se mai tale ipotetica formula matematica fosse davvero esistita, qualcuno di voi l'avrebbe conosciuta di sicuro...ma di  certo non io.
Per quanto riguardava (e riguarda) le mie limitate conoscenze "geometrico-matematiche", infatti, secondo me è IMPOSSIBILE  trovare l'area di un rettangolo, conoscendone soltanto il perimetro.
E, almeno in questo caso, la mia convinzione ha trovato conferma anche in chi è MOLTO più esperto di me.
***
Per questo, in seguito, avevo scritto che io "non ho mai sostenuto di poter trovare l'area di un rettangolo, conoscendone soltanto il perimetro! Mai!"
Il che è vero.
***
Un saluto! :)
***
P.S.
Scusa se ho confuso i post. 
#1872
Percorsi ed Esperienze / Re: Il rebus del "parquet"!
14 Marzo 2023, 12:39:23 PM
Ciao Bomax :)
In ordine alle tue ripetitive infondate affermazioni, benchè, come diceva Shakespeare, sia  "tempo perso cercare di lucidare il ghiaccio", non posso esimermi dal ribadire l'ovvio.
E, cioè, quanto segue:
.
1)
I dati che costituiscono il presupposto di un ragionamento, sono una cosa diversa dal ragionamento stesso, anche se ne costituiscono la base; questa è una verità "universalmente" accettata.
Ed invero tutti i "perimetri" sono espressi in centimetri lineari, per cui non serve nessun ragionamento per appurare o definire una simile ovvietà; sarebbe come dire che per per accertare se un quadrupede ha quattro zampe, bisogna contare le due davanti e le due di dietro, e poi fare la somma (oppure contarle una per una). :D
Per sapere che tutti i "perimetri" sono espressi in centimetri lineari, basta conoscere il significato della parola "perimetro" in lingua italiana, senza dover fare nessun ragionamento!
Punto!
.
2)
Tu scrivi "Leggi la parola "perimetro" e il numero 28,8 e ne deduci che si riferiscano al tassello."; ma hai dimenticato di precisare che la parola "perimetro" e il numero 28,8 sono scritti proprio sul tassello, e non da un'altra parte.
A volte mi viene il dubbio che tu voglia burlarti di me! ;)
E' ovvio che se trovo la parola "perimetro" e il numero 28,8 cm "scritti su un tassello",  è evidente che tali dati si riferiscono al tassello stesso, e non al perimetro del pene del piastrellista; non occorre fare nessun "ragionamento" per doverlo "dedurre".
Sarebbe come dire che, quando vedi che su una porta c'è scritto SPINGERE, tu ti devi mettere a "ragionare", per "dedurre" che è la porta che bisogna "spingere", e non la signora che sta davanti a te! :D
Dire: "Leggi la parola "perimetro" e il numero 28,8 su un tassello, e ne deduci col ragionamento si riferiscano al tassello.", è come scrivere: "Incontri uno per strada, che ti prende per il bavero e ti dice che sei uno scemo, ma tu devi fare un "ragionamento" per dedurre" che si sta rivolgendo a te. :D
Se non riesco a spiegarmi nemmeno con questi esempi, ci rinuncio
.
3)
Quanto alla mia sfiducia non è nei tuoi confronti, ma in alcune tue argomentazioni che trovo del tutto prive di senso; il tuo calcolo, invece, lo trovo assolutamente corretto, (anche se incompleto) come ho più volte ribadito.
Sei tu, invece, che non hai mai ammesso che anche il mio lo è; benchè dia un risultato identico a quello tuo.
Perchè mai?
.
4)
Comunque non penso affatto che ciò che scrivi sia un atto ostile verso di me; semmai lo è verso te stesso, quando ti ostini a sostenere assunti insostenibili, i quali, a volte, rasentano il ridicolo!
.
5)
Se vi è una carenza di "logica", infatti, è sicuramente da parte tua;  dovuta, forse, ad una tua eccessiva erudizione "matematica".
Per questo la tua reazione è di chiusura e rigetto; e resta così la solita confusione.
Ritengo perciò inutile anch'io proseguire ogni altra interazione.
.
***
Un saluto :)
***
#1873
Percorsi ed Esperienze / Il mistero del gatto!
14 Marzo 2023, 11:44:40 AM
Tranquilli, questa volta non si tratta di un enigma geometrico o matematico, bensì di una esperienza personale, che, all'inizio, avevo trovato davvero misteriosa; ma che, essendo abbastanza singolare, credo che meriti comunque di essere raccontata.
***
Ierisera, verso le 11, dormivo profondamente, quando la mia "compagna di letto" (che era rimasta sveglia a guardare la televisione in salotto), entra in camera ed accende bruscamente la lampada sul mio comodino, dicendomi perentoriamente:
-Guarda! Ti piace il mio regalino?-
Aprendo a fatica gli occhi, mezzo accecati dalla luce, vedo che mi ha posato un gattino scolpito in legno sul comodino; tra l'Augmentin e la radiolina portatile.
- Grazie!- le faccio prendendolo un attimo in mano per dargli un'occhiata, e poi rimettendolo subito a posto - E' molto carino, ma adesso vorrei dormire!-
- Certo!- mi fa -Ma prima fotografalo col tuo cellulare-.
E me lo mette in mano (il mio cellulare, non il gattino).
***
- E perchè mai dovrei fotografarlo?- chiedo io interdetto.
- Domani te lo spiego- risponde - Ma adesso fallo!-
Senza neanche alzare la testa dal cuscino, la accontento, realizzando la seguente fotografia (non certo eccezionale):
***
Il giorno dopo, vengo svegliato a sole appena sorto, e lei mi fa: - E adesso fotografalo alla luce del giorno!-
Senza neanche stare a discutere, obbedisco, e, sempre dalla stessa posizione, ottengo una foto un tantino migliore di quella della sera precedente.
***
- Non noti nessuna differenza rispetto a ieri?- mi chiede.
- Sinceramente no!- rispondo perplesso.
- Ecco perchè te l'ho fatto fotografare sia ieri che oggi: confronta le due foto!-
***
Lo faccio, e, allora, mi accorgo che, effettivamente, una differenza c'è!
Eccolo tenuto anche in mano.
***
Voi come ve la spiegate la differenza, ammesso che l'abbiate notata?
***
#1874
Percorsi ed Esperienze / Re: Il rebus del "parquet"!
14 Marzo 2023, 07:04:25 AM
Ciao Bobmax. :)
In ordine al tue nuove considerazioni, ritengo di poter osservare quanto segue, invitandoti a leggere il mio seguente post con più attenzione di quanto tu non abbia fatto in precedenza (senza offesa); mi scuso per la mia prolissità, ma è resa necessaria dalla tua ostinazione nel voler negare alcune evidenze!
.
1)
Tu scrivi: "Mi viene un dubbio, perchè da quello che scrivi sembra tu creda di essere riuscito a ricavare l'area del tassello conoscendo SOLTANTO il suo perimetro. E' così? Nel caso ti dico che ti sbagli!"
A me, invece, viene il dubbio che, mentre io ho capito perfettamente il tuo (corretto) ragionamento, tu non hai capito assolutamente "niente" del mio, che pure è egualmente semplice e corretto; e, questo, nonostante che io lo abbia ripetutamente spiegato, ed illustrato persino con un disegno esplicativo.
***
Ed infatti, se tu lo avessi compreso, non ti saresti mai sognato di supporre "che io creda di essere riuscito a ricavare l'area del tassello conoscendo SOLTANTO il suo perimetro"; il che è assolutamente IMPOSSIBILE.
Io, invece, sono partito da una diversa considerazione che mi sembrava ovvia; e, cioè, che, se il "perimetro" del tassello è di 28,8 cm, il suo "semiperimetro" A_C_D non poteva essere che di 14,4 cm.
Per cui, visto che i tasselli sono tutti della stessa "identica forma geometrica" e della stessa "identica dimensione", questo significa che il "semiperimetro" A_C_D di 14,4 cm, deve essere lungo esattamente come il segmento di retta che va da C ad E; ed infatti A_C o B_D  devono necessariamente essere uguali a D_E, come risulta evidente dalla seguente immagine.
Ed infatti i lati corti dei tasselli, devono avere tutti la stessa identica lunghezza!
Da tale immagine risulta pure che il segmento di retta lungo 14,4 cm, che va da C ad E,  "corrisponde" esattamente a 6 "lati corti" dei tasselli; per cui il lato corto di ciascun tassello (compresa l'altezza del tassello di partenza), deve necessariamente essere di 2,4 cm, perchè 14,4 diviso sei dà 2,4. .
Per cui l'area del nostro tassello di partenza, è di 28,8 cmq (12 x 2,4).
***
Quindi, è ovvio che anche io, come te, ho sfruttato dei dati ulteriori oltre a quello del solo perimetro!
***
Ed infatti, espresso in formula il ragionamento di cui sopra, data X come incognita da trovare, e, cioè,  l'"area del tassello" (da cui poi ricavare, per moltiplicazione, sia quella di una singola mattonella, sia quella  di tutte e nove le mattonelle);
Dato P, come perimetro noto del tassello;
Dati come identici tutti i tasselli;
Dato LC come lato corto del tassello;
Dato LL come lato lungo del tassello;
Avremo:
P/2/6 = LC (2,4 cm Lato Corto del tassello)
LC x 5 = LL  (12 cm Lato Lungo del tassello)
LC x LL = X (, cioè,  l'"area del tassello" di 28,8 cmq)
***
Quindi, mi sembra palese che anche io, come te, ho sfruttato dei dati ulteriori oltre a quello del solo perimetro; solo che ho fatto un ragionamento diverso dal tuo, sebbene egualmente valido!
Ma non ho mai sostenuto di poter trovare l'area di un rettangolo, conoscendone soltanto il perimetro!
Mai!
***
.
2)
Se siamo riusciti entrambi a risalire all'area del tassello è perchè avevamo "svariati" elementi di calcolo a disposizione, dei quali tu ne hai utilizzato alcuni, mentre io altri; ma la circostanza che entrambi siamo pervenuti alle stesse identiche soluzioni, dimostra inequivocabilmente che entrambi i nostri procedimenti erano del tutto corretti.
.
3)
Tu scrivi che: "Per ''dati'' va inteso l'insieme delle informazioni che abbiamo sul problema indipendentemente dalla loro forma, che può essere numerica o meno."
Secondo me, invece, è molto più chiaro dire che, per "dati" di un determinato problema, si intendono le "informazioni" che ci vengono fornite "a priori" per poter risolvere il problema che ci è stato posto; il quale consiste nel trovare le "soluzioni" non conosciute (incognite), che si possono individuare "a posteriori" attraverso il ragionamento e il calcolo basati sui "dati" che ci sono stati forniti.
.
4)
Non c'è nessun "intoppo" nè nel mio ragionamento nè nel tuo, per risolvere il problema che ci è stato posto; ed infatti lo abbiamo risolto entrambi, sia pure seguendo strade diverse.
Dimmi che adesso, finalmente, lo hai capito!
.
5)
Tu scrivi: "Eutidemo, da quanto scrivi mi appare evidente che per te i dati iniziali non sono frutto di un ragionamento."
Certo che non lo sono, come non lo sono per nessun altro; te compreso!
Ed infatti, per "dati" di un determinato problema, si intendono le "informazioni" che ci vengono gentilmente fornite  per poter risolvere il problema che ci è stato posto, e che non sono assolutamente frutto di un nostro ragionamento.
Ed infatti, per sapere "a priori" che il perimetro del tassello era di 28,8 cm,  non ho certo dovuto fare nessun "ragionamento", ma mi è bastato leggerlo sul sul lato posteriore.
.
6)
Invece, assurdamente, tu scrivi: "Il perimetro di 28,8 viene inteso, tramite il ragionamento che si  tratta di 28,8 cm lineari."
Santo cielo!
Tutti i "perimetri" sono espressi in centimetri lineari, per cui non serve nessun ragionamento per appurare una simile ovvietà; sarebbe come dire che per per accertare se un quadrupede ha quattro zampe, bisogna contare le due davanti e le due di dietro, e poi fare la somma (oppure contarle una per una). :D
Per sapere che tutti i "perimetri" sono espressi in centimetri lineari, basta conoscere il significato della parola "perimetro" in lingua italiana, senza dover fare nessun ragionamento!
.
7)
Che le mattonelle siano quadrate, invece, quello sì che il risultato di un ragionamento; come pure che il lato minore di un tassello sia 1/5 del lato maggiore!
Ma sono cose diverse dal "perimetro"!
Dato, quest'ultimo, che non abbiamo minimamente dedotto da nessun ragionamento, ma che ci è stato gentilmente fornito dal piastrellista; altrimenti non avremmo potuto fare nessun calcolo, se non usando il centimetro.
.
8 )
Poi tu scrivi: "E come fai allora a scrivere P/2/6 = LC ? Donde nasce quel 6? Non deriva forse da un ragionamento?"
Certo che sì!
Si tratta di un "ragionamento" che, però, è stato sviluppato partendo dal "dato" noto P 28,8 cm (perimetro) che mi era stato fornito dal piastrellista; se non avessi conosciuto la misura di P, il mio ragionamento non sarebbe stato in  piedi.
E nemmeno il tuo.
.
9)
Il considerare i "dati iniziali" esistenti grazie ad  un nostro ragionamento, porta ad ingenerare una terribile confusione; come il protrarsi di questa ormai stucchevole discussione dimostra ampiamente.
Ma come diamine fai a sostenere che i "dati iniziali" di un problema, fornitici da "altri", siano il frutto di un "nostro" ragionamento?
Boh!
.
10)
Poi tu scrivi: "L'accusare poi di incompletezza perché non è stata esplicitata l'area (dato omesso per semplicità e anche perché le elementari sono ormai passate da un pezzo) mostra ancor più l'inutilità di partecipare."
Al riguardo, evidentemente, abbiamo due concezioni completamente diverse della "completezza", della "congruità" e dell'"esaustività" di una esposizione, sia essa logica, matematica o semplicemente argomentativa.
Ad esempio, se io ti pongo il seguente problema: "Considerato un quadrato di 101.808 cm di perimetro, qual'è la sua area?", tu che cosa mi rispondi "Il lato e di 25.452, e mo' l'area calcolatela da solo"?
Andiamo, siamo seri!
.
***
Un saluto! :)
***
.
P.S.
Quanto alla mia prolissità, è resa necessaria dalla circostanza che tu, pur avendo effettuato un calcolo correttissimo:
- ti ostini a negare la correttezza del mio;
- fai affermazioni del tutto assurde, (come, ad esempio, il fatto che i "dati iniziali" di un problema, fornitici da "altri", siano il frutto di un "nostro" ragionamento)
#1875
Percorsi ed Esperienze / Re: Il rebus del "parquet"!
13 Marzo 2023, 17:31:58 PM
Ciao Bobmax. :)
In ordine al tue nuove considerazioni, ritengo di poter osservare quanto segue:
.
1)
Proprio perchè i "dati" sono già "dati" (cioè "conosciuti") prima di risolvere il "problema", non occorre applicare nessun "ragionamento"  per riuscire a definirli (così come scrivi tu); ed infatti essi sono già determinati in anticipo.
Ad esempio, non occorre applicare nessun "ragionamento"  per riuscire a determinare il "perimetro" del tassello, perchè tale "dato" è già scritto sul suo retro; ed è sulla base di tale "dato" (oltre all'identicità dei tasselli) che dobbiamo costruire il nostro "ragionamento" per risolvere il problema che ci siamo posto.
Per usare un abusato luogo comune, cioè:
- i "dati" sono "a monte";
- i "ragionamenti" sono "a valle".
.
2)
Poi tu scrivi:
"La mia equazione originaria diceva già tutto. Avevo comunque aggiunto la soluzione: x = 12. Che altro serviva? Nient'altro!"
Ma non è affatto così!
Ed infatti, come avevo scritto nel mio TOPIC iniziale, io mi ero riproposto di "scoprire se, conoscendo soltanto il "perimetro" di quel singolo tassello, fosse possibile ricostruire  non solo l'"area di quel tassello" o  l'area  della singola "mattonella di cinque tasselli", ma, addirittura, l'"area di nove mattonelle" (di cinque tasselli ciascuna) affiancate."
Ed invece la tua equivalenza X = 12 cm indicava soltanto il lato lungo di un tassello, uguale al lato di una mattonella; il che è corretto, ma a quel punto tu "ti sei fermato" non dando nessuna delle soluzioni richieste nel topic.
E cioè:
1) area del tassello
2) area della mattonella
3) area dell'intero spazio fotografato
Ora lasciamo perdere 2) e 3), che sono soluzioni scontate, ma almeno la "soluzione base" 1), cioè l'area del tassello di 28,8 cmq, quella, almeno, la dovevi dare.
Ed invece la tua equivalenza X = 12 cm indicava soltanto il lato lungo di un tassello, uguale al lato di una mattonella, ma non certo l'area del tassello; anche se, per farlo, ti sarebbe bastato un piccolo sforzo in più.
Ed infatti, seguendo il tuo stesso metodo, avresti potuto facilmente calcolare l'area della mattonella, moltiplicando lato per lato; e poi dividendo per cinque, ottenere così l'area del tassello di 28,8 cmq .
.
3)
Poi tu scrivi: "aggiungendo non può che alla fine crescere la confusione."
Il che può essere senz'altro vero in certi casi, ma non quando si deve doverosamente precisare se 28,8 sono "centimetri lineari" o "centimetri quadrati"; ed infatti è una regola universalmente seguita che i "numeri che esprimono una misura, devono SEMPRE essere seguiti dall'unità di misura adottata".
.
4)
Quanto al fatto che la mia "distrazione"  e la mia "sbadataggine" crescente siano davvero un dono,  anche se ancora non me ne avvedo, ho i miei seri dubbi.
Però potrebbe anche essere!
.
5)
Il mio domandare e domandarmi in continuazione le cose più strane, invece:
- in parte è frutto della mia innata maniacale curiosità per tutto (che mi perseguita sin da ragazzo);
- in parte, invece, specie per quanto riguarda le mie curiosità più futili, credo che sia soprattutto frutto del mio rimbambimento senile (che mi perseguita  soprattutto da vecchio).
***
Per concludere, provando invidia per te e per Iano, voglio provare anche io a inventarmi un'equazione; però vi prego di non mettervi a ridere.
------------------------------------------------------
Data X come incognita da trovare, e, cioè,  l'"area del tassello" (da cui poi ricavare, per moltiplicazione, sia quella di una singola mattonella, sia quella  di tutte e nove le mattonelle);
Dato P, come perimetro noto del tassello;
Dati come identici tutti i tasselli;
Dato LC come lato corto del tassello;
Dato LL come lato lungo del tassello;
Avremo:
P/2/6 = LC (2,4 cm)
LC x 5 = LL  (12 cm)
LC x LL = X (, cioè,  l'"area del tassello")
------------------------------------------------------------
***
Un saluto :)
***
Pagine 1 ... 123 124 125 126 127 ... 410