Menu principale
Menu

Mostra messaggi

Questa sezione ti permette di visualizzare tutti i messaggi inviati da questo utente. Nota: puoi vedere solo i messaggi inviati nelle aree dove hai l'accesso.

Mostra messaggi Menu

Messaggi - Eutidemo

Pagine 1 ... 126 127 128 129 130 ... 410
#1906
Tematiche Filosofiche / Re: Il paradosso dell'area del quadrato
04 Marzo 2023, 15:55:37 PM
Ciao Iano. :)
Quello che scrivi è tutto vero; ma, in questo caso, non si tratta di un paradosso dovuto al concetto di "infinito" o agli "infinitesimali" (che sono un'altra cosa), come il paradosso della "Freccia" o quello di "Achille e la tartaruga", bensì di una "contraddizione" tra due formule matematiche che partono entrambi da numeri finiti, limitati e ben definiti: 2 METRI!
***
Ed infatti, avendo un quadrato di due metri lineari "esatti" di lato:
.
a)
Se moltiplichiamo lato per lato, otterremo che il quadrato avrà un'area di 4,00 metri quadrati "esatti".
.
b)
Se, invece, basandoci "sugli stessi identici  due lati di 2 mt esatti", ricaviamo, per mezzo della loro ipotenusa, la diagonale del quadrato, in base alla formula della diagonale alla seconda potenza diviso 2, otterremo che il quadrato avrà un'area di 3.97 metri quadrati "approssimati".
.
***
Il che dovrebbe essere logicamente impossibile!
***
Un saluto! :)
***
#1907
Racconti Inediti / Re: Diamonologo
04 Marzo 2023, 10:55:45 AM
Citazione di: iano il 04 Marzo 2023, 01:57:19 AMForse non ci aiuterà a rispondere alla domanda porla in termini meno spettacolari., ma secondo me la vera domanda è: ''Se cambio un solo pezzo della nave ho la stessa nave?''


Bella domanda!
Secondo me, la risposta può essere data, in modo diverso, a seconda per "piano" prescelto:
- a livello "teorico",  se tu cambi anche un solo qualsiasi pezzo della nave, non hai più la stessa identica nave (come tu non sei più esattamente quello di prima, se subisci un trapianto di cuore);
- a livello "pratico", invece,  non hai più la stessa nave solo se cambi un pezzo davvero identificativo della nave originaria (come  tu sei sempre quello di prima, anche se subisci un trapianto di cuore).
 Un saluto :)
#1908
Tematiche Filosofiche / Re: Il paradosso dell'area del quadrato
04 Marzo 2023, 10:41:40 AM
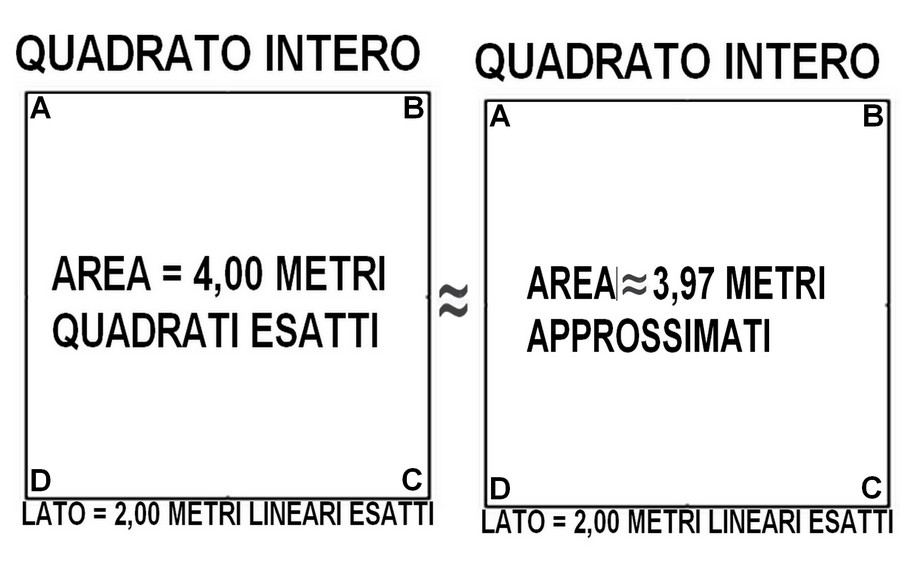
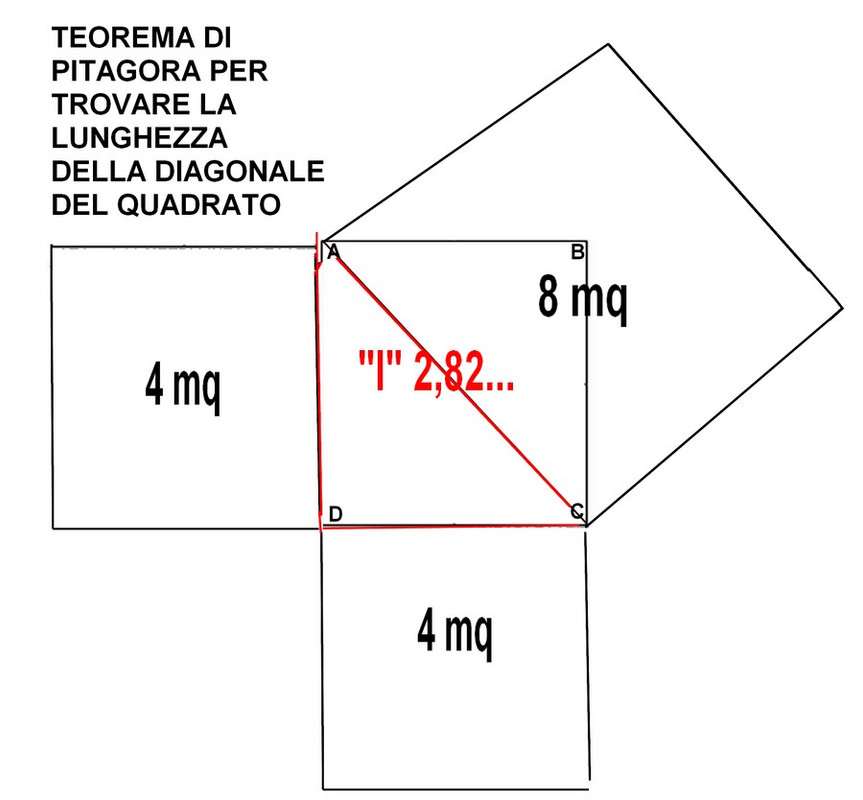
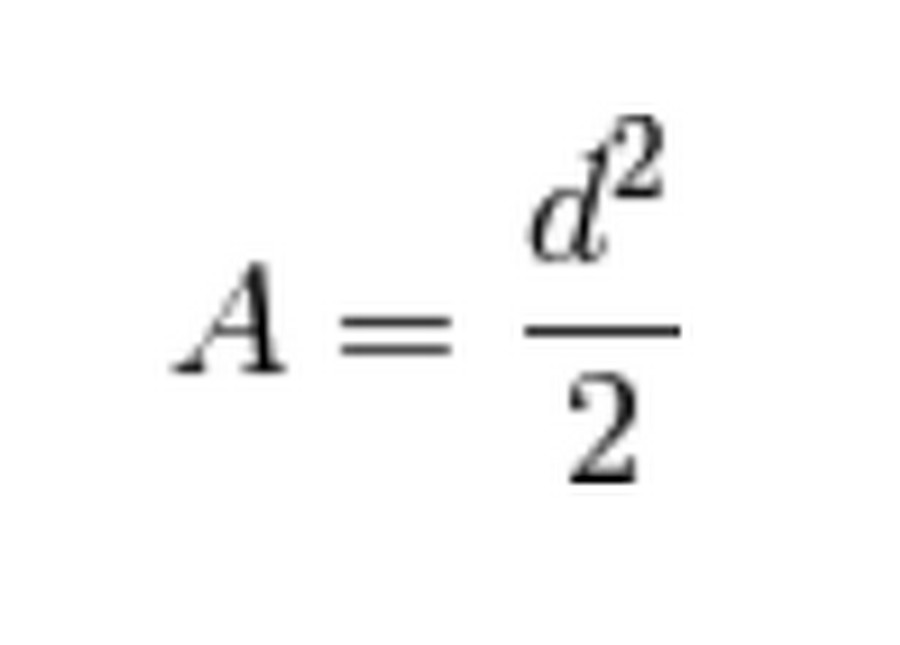Ciao Bobmax :)
A parte la mia "rara facoltà di chiarire l'esistente", che mi sembra che tu "sopravvaluti" in modo davvero "eccessivo", per il resto sono pienamente d'accordo su tutto il resto che hai scritto in questo post.
Soprattutto sul fatto che "non vi è nessun fenomeno che non sia (manifestazione transeunte dell') ESSERE", e che per noi "è ormai giunto il momento di tirare le somme, e di prepararci per tornare all'Uno".
Per me non ci manca molto!
***
Un saluto! :)
***
#1909
Tematiche Filosofiche / Re: Il paradosso dell'area del quadrato
04 Marzo 2023, 10:29:56 AM
Citazione di: iano il 04 Marzo 2023, 08:32:00 AMPlatone però c'è riuscito.
Confesso che questa mi era sfuggita; puoi darmi il riferimento per cortesia?
Cosa ne pensi del mio paradosso del quadrato? :)
#1910
Storia / Re: Il beccamorto
04 Marzo 2023, 06:27:13 AM
Ciao Pensarbene. :)
La tua spiegazione dell'origine e della ragione del nome "beccamorto", è interessante ed è del tutto storicamente veritiera.
Però è errata la tua prima immagine, perchè, quella specie di "becco" indossato sul volto, non serviva certo a "beccare" il morto, ma aveva una funzione analoga a quella delle attuali "mascherine" anticovid.
Vedi, al riguardo, il seguente LINK:
https://www.nationalgeographic.it/storia-e-civilta/2020/03/il-mistero-della-macabra-maschera-forma-di-becco-dei-medici-della-peste
***
Un saluto :)
***
#1911
Percorsi ed Esperienze / Re: Il paradosso del cubo
04 Marzo 2023, 06:11:28 AM
Citazione di: iano il 04 Marzo 2023, 01:37:21 AMVero, la nostra esperienza determina la probabilità di ciò che vedremo.
Così nel caso di una semisfera concava, che disegneremo allo stesso modo di una sfera convessa, essendovi equiprobabilità, lo sforzo dobbiamo farlo per mantenere fissa una visione, che diversamente passerà in continuazione da una percezione all'altra.
Vedremo cioè la convessità divenire concavità e poi convessità etc in continuo.
Ciò perchè vedremo convessità o concavità asseconda da dove immaginiamo provenga la luce, e nella nostra esperienza la luce può venire ugualmente da tutte le direzioni.
E' verissimo!
Guarda questa Illusione ottica della maschera di Charlie Chaplin:
https://www.youtube.com/watch?v=JLgXTzbZpDQ
#1912
Tematiche Filosofiche / Re: Il paradosso dell'area del quadrato
04 Marzo 2023, 06:02:26 AM
Ciao Bobmax
Dire che "è la rappresentazione ad essere inesatta, e non il numero in sè, per cui √2 è esatto", non è logicamente corretto come dire che, nell'Otello di Gassman "è la rappresentazione di Jago effettuata da  Salvo Randone ad essere malvagia, e non Salvo Randone  in sè, per cui Salvo Randone  è buono".
***
Ed infatti:
- mentre è possibile distinguere l'attore Salvo Randone dal personaggio (Jago) che lui "rappresenta";
- come diamine è possibile distinguere un numero dalla sua "rappresentazione"?
Non ci riuscirebbe neanche Schopenhauer!
***
Il tuo, quindi, per quanto indubbiamente  "elegante" è solo un "artifizio sofistico" privo di qualsiasi efficacia dimostrativa!
***
Hai invece perfettamente ragione quando scrivi che "i concetti van tenuti ben fermi, perchè lo pretende la logica; in caso contrario non può che nascere la confusione".
Però è un consiglio che tu dovresti seguire per primo! ;)
***
Bada bene che io sono il primo a pensare che, nel mio ragionamento, ci sia qualcosa che non "quadra"; ma non certo per quello che scrivi tu!
***
Comunque ti ringrazio per aver provato a chiarirmi le idee; anche se con scarsa fortuna.
Non è colpa tua se i tuoi argomenti non mi convincono affatto; per cui non devi offenderti se dissento da essi in modo così drastico!
Ti rinnovo infatti la mia stima, perchè, di solito, trovo le tue argomentazioni (quasi) sempre molto convincenti!
***
Un saluto! :)
***
#1913
Tematiche Filosofiche / Re: Il paradosso dell'area del quadrato
03 Marzo 2023, 17:34:45 PM
Ciao Bobmax. :)
Tu scrivi che "I numeri irrazionali sono esatti"; il che, invece, è assolutamente "inesatto", come potrai riscontrare in qualsiasi libro di matematica.
Ed infatti, considerato che la rappresentazione decimale dei numeri irrazionali è spesso infinita e non può mai essere espressa come un numero finito, ne consegue matematicamente, logicamente e grammaticalmente, che "i numeri irrazionali non sono mai esatti, ma solo approssimati"
***
Inoltre, dire che i numeri irrazionali sono esatti, ma non è mai esatto il loro calcolo, è una contraddizione in termini; che non ha alcun senso nè matematico nè logico.
***
Tanto più che, poi, ammetti che non è possibile calcolare esattamente la diagonale; il che vuol proprio dire dire che √2 del lato non è esatto, ma solo "approssimato".
Tanto è vero che √2 è utilizzato proprio come esempio per rappresentare il simbolo "circa".
***
Ora devo uscire e torno tardi perchè ceno fuori; quindi spero di non avere altri dormiveglia del genere questa notte, perchè non credo che gli altri commensali mi consentiranno di parlare di questa roba.
***
Un saluto :)
***
#1914
Tematiche Filosofiche / Re: Il paradosso dell'area del quadrato
03 Marzo 2023, 17:12:26 PM
Ciao Atomista Pentito (di aver letto il mio topic). :)
Mi dispiace di averti fatto venire il mal di testa -addirittura in tedesco-, leggendo il mio topic; però, come si suol dire "mal comune mezzo gaudio", perchè, scrivendolo, il mal di testa era venuto anche a me! ::)
***
Quanto al fatto che una persona nel dormiveglia abbia questo tipo di stimoli (il che è vero, e non una battuta), forse dovrebbe suggerire a tale persona di andare in visita da uno psichiatra; ma da uno veramente bravo!
***
Quanto al "grande", forse il tuo è un refuso: una "r" al posto di una "l" (come spesso viene definita la mia testa)
***
Ed invero, conoscendo il lato esatto di un quadrato, e, quindi, la sua area esatta con una semplice moltiplicazione (2x2), solo una "testa di glande" come il sottoscritto poteva arrovellarsi a trovare la diagonale del quadrato (approssimata), per ricavarne un'area (approssimata) dello stesso quadrato, diversa da quella esatta.
***
Un saluto! :)
***
#1915
Tematiche Filosofiche / Re: Il paradosso dell'area del quadrato
03 Marzo 2023, 16:51:41 PM
Ciao Bobmax :)
Tu scrivi: "La diagonale è √8. Questo è il valore esatto."
Ma non è così, perchè la radice quadrata di 8 è un "numero irrazionale"; e, quindi, è senz'altro un "valore inesatto".
.
***
Elevando al quadrato 2,82 (I), otteniamo 7,95 (I), che, diviso per due, da 3,97 (I).
***
.
***
Per cui, avendo un quadrato di due metri lineari "esatti" di lato:
.
a)
Se moltiplichiamo lato per lato, otterremo che il quadrato avrà un'area di 4,00 metri quadrati "esatti".
.
b)
Se, invece, basandoci "sugli stessi identici  due lati di 2 mt esatti", ricaviamo, per mezzo della loro ipotenusa, la diagonale del quadrato, in base alla formula di cui sopra, otterremo che il quadrato avrà un'area di 3.97 metri quadrati "approssimati".
***
Per cui non è affatto vero, come tu scrivi che:
- "L'esatto deriva sempre e comunque dall'esatto", perchè, in questo caso, l'"inesatto" (l'ipotenusa) scaturisce matematicamente dall'"esatto" (il lato)
- "Se approssimi la diagonale, allora pure i lati dovranno necessariamente essere approssimati", perchè, in questo caso, ad una diagonale "approssimata", corrispondono dei lati assolutamente "esatti".
.
***
Ed infatti io sono matematicamente pervenuto ad una "diagonale approssimata", partendo da due lati che non sono affatto "approssimati", bensì sono assolutamente "esatti"!
***
.
Detto in altre parole, non sono io che "scelgo di approssimare la diagonale", in quanto "è la diagonale a scaturire automaticamente approssimata" per conto suo; il che si verifica matematicamente, estraendo la radice quadrata del quadrato costruito sull'ipotenusa, ottenuto sommando i quadrati costruiti sui cateti, secondo il teorema di pitagora (cateti che hanno due metri "esatti" di lato).
***
Un saluto! :)
***
#1916
Tematiche Filosofiche / Il paradosso dell'area del quadrato
03 Marzo 2023, 12:24:18 PM
Mi dovete scusare, ma il "demone della matematica", in compagnia del "demone della geometria", debbono recentemente avermi "invasato"; forse perchè in gioventù li avevo trascurati troppo.
Così, questa notte, nel dormiveglia, mi hanno tormentato con un (presunto) "paradosso dell'area del quadrato"; il quale, da sveglio, ho cercato di risolvere razionalmente da solo, ma senza riuscirci.
Per cui adesso io tormento voi, sperando che riusciate a spiegarmi:
- laddove si nasconda l'erronea impostazione del mio ragionamento.
- laddove io abbia sbagliato qualche semplice calcolo.
Sempre che abbiate voglia di stare a perderci tempo!
.
***
Consideriamo (beninteso non, materialmente, in "fisica", bensì in "geometria") un quadrato che ha un lato lungo due metri lineari "esatti"; il quale, quindi, come ho imparato alle elementari, avrà un'area di quattro metri quadrati "esatti".
***
Ed ora dividiamolo per due, nel modo più semplice possibile; e, cioè, tagliandololo a metà con la "diagonale AC".
***
Per ottenere la lunghezza sua "diagonale AC",  che lo taglia in due parti uguali, dobbiamo rifarci al "Teorema di Pitagora";  il quale afferma che in un triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa (lato opposto all'angolo retto) equivale alla somma delle aree dei quadrati costruiti sui cateti (gli altri due lati del triangolo, che, nel nostro caso, corrispondono a due lati del quadrato).
***
Dal "Teorema di Pitagora" possiamo quindi  pervenire alla formula che ci permetterà di calcolare il valore della diagonale del quadrato.
E cioè:
- visto che  AC² = AB² + BC²;
- visto che si tratta di un quadrato, i lati sono tutti congruenti fra loro, dunque AB = BC = lato;
- per cui AC² = lato² + lato² ;
- e pertanto, per ottenere la diagonale AC, basterà calcolare la radice quadrata del quadrato costruito sull'ipotenusa (AC = √(lato² + lato²) = √2lato² = lato√2).
In conclusione, quindi,  giungiamo alla conclusione che la diagonale del quadrato corrisponde anche al lato 2 moltiplicato per la √2.
Cioè: 2 x 1,41(4213562373095...) cioè, "circa" 2,82... metri lineari.
***
Ed infatti la radice quadrata di 2 è un numero irrazionale: 1,41...
***
D'altronde, anche la radice quadrata del  quadrato costruito sull'ipotenusa, cioè la radice quadrata di 8 mq, ci dà circa il doppio dello stesso numero irrazionale  di 1,41(4213562373095..,e, cioè, 2,82(842712474619...), che pure è un numero irrazionale.
.
***
Ma io, dai miei ricordi scolastici, sapevo se è nota la misura della diagonale del quadrato, per calcolare l'area del quadrato, si deve elevare la misura della diagonale alla seconda e dividere il risultato per 2, secondo la nota formula matematica: cioè, 2,82 x 2,82 = 7,95 :2 = 3,97 (tutto "I")
***
Abbiamo così un "risultato paradossale", e, cioè, che avendo a disposizione un quadrato (geometrico) di due metri lineari "esatti" di lato:
.
a)
Se moltiplichiamo lato per lato, otterremo che il quadrato avrà un'area di 4,00 metri quadrati "esatti".
.
b)
Se, invece, basandoci sugli stessi due lati, ricaviamo, per mezzo della loro ipotenusa, la diagonale del quadrato, in base alla formula di cui sopra, otterremo che il quadrato avrà un'area di 3.97 metri quadrati "approssimati".
.
***
Ma mi sembra logicamente "impossibile" che, uno stesso quadrato, abbia nello stesso tempo un'area di 4 mq "precisi", e, nello stesso tempo, anche, un'area 3.97 metri quadrati "approssimati", a seconda che, basandosi sugli stessi due lati, si ricorra a due diverse formule matematiche universalmente accettate come valide per determinare l'area dello stesso identico quadrato.
***
.
***
Per cui, i casi sono tre:
a)
O io ho sbagliato completamente l'impostazione del mio ragionamento.
b)
O non ho sbagliato completamente l'impostazione del mio ragionamento, ma ho sbagliato qualche calcolo.
c)
Oppure c'è un contrasto tra:
- la formula per calcolare l'area del quadrato moltiplicando la lunghezza di un lato per la lunghezza dell'altro;
- la formula per calcolare l'area del quadrato ricavandolo dalla lunghezza dell'ipotenusa;
- il teorema di Pitagora.
***
.
***
Ritengo molto più probabili le ipotesi sub a) o b); nel qual caso gradirei molto se qualcuno, molto più esperto di me in matematica, mi spiegasse il mio errore/i. ;)
***
#1917
Tematiche Spirituali / Re: La Bibbia e l'eutanasia
03 Marzo 2023, 05:38:20 AM
Ciao Taurus :)
Hai ragione, è tutto verissimo; però c'è una grossa differenza tra  Giobbe e Qoheleth.
.
a)
Giobbe era stato vittima di una "sfiga" tremenda; per cui chiunque al suo posto si sarebbe amaramente lamentato.

.
b)
A Qoheleth, invece (che sembra fosse re Salomone), "era sempre andata l'acqua per l'orto"; però, nonostante che tutto gli fosse andato per il verso giusto, nella sua leggendaria saggezza si rese conto che la vita era comunque  una grossa "fregatura", e che, quindi, sarebbe stato meglio non nascere affatto!

.
***
Un saluto!  :)
***
#1918
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
03 Marzo 2023, 05:22:36 AM
A dire il vero, per sapere se la data area di un quadrato è matematicamente "approssimata" o "esatta", è sufficiente estrarre la sua radice quadrata, senza poi necessariamente doverla moltiplicare per se stessa.
***
Ed infatti:
a) Se il risultato della radice quadrata è "Q" (cioè un "numero naturale"), ciò significa che la la data area è "esatta".
b) Se, invece, il risultato della radice quadrata è "I" (cioè un "numero irrazionale"), ciò significa che la la data area è soltanto "approssimata".
***
Se è così, cosa di cui chiedo conferma a chi più esperto in materia di me, il mio "teorema" è esatto; però costituisce una inutile "superfatazione" di calcoli. :(
E' giusto?
***
#1919
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
02 Marzo 2023, 16:57:28 PM
Citazione di: iano il 02 Marzo 2023, 12:19:17 PMBalle, vero è che ci manca solo il tempo, ma non che quello che ci rimanga sia in tal modo mal impiegato.
Il pensiero ci mette tempo a cambiare, è vero, anche millenni, ma in fondo cos'è il piacere di pensare se non il sorprendersi a cambiare il proprio pensiero.
Hai ragione tu! ;)
O, almeno, spero che sia così anche per me ::)
#1920
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
02 Marzo 2023, 16:52:45 PM
Ciao Phil. :)
E' vero che, un quadrato di 5024 m2,  essendo "approssimato", è inevitabile che sia approssimata anche ogni suddivisione che venga praticata in seguito (e viceversa); ma poichè non sempre le aree vengono indicate specificando se si tratta di misure "esatte" o "approssimate", credo che la mia formula possa servire a verificarlo matematicamente.
***
Tecnicamente il simbolo "circa", andrebbe usato anche per i calcoli con il pi greco; ma non tutti lo fanno, in quanto il pi greco è approssimato "per antonomasia" (come nel logo di YOUMATH).
In altri casi, invece, la cosa non è così evidente!
***
Peraltro:
- le aree dei cerchi, essendo calcolate tutte con il pi greco, non c'è neanche bisogno di verificare se siano approssimate o meno, perchè lo sono "tutte";
- le aree dei quadrati, invece, non lo sono affatto "tutte", ma possono essere approssimate oppure esatte, per cui, per verificarlo, pensavo che la mia "formuletta di riscontro" potesse risultare utile.
***
Ma era solo un'idea da profano!
***
Un saluto! :)
Pagine 1 ... 126 127 128 129 130 ... 410