Menu principale
Menu

Mostra messaggi

Questa sezione ti permette di visualizzare tutti i messaggi inviati da questo utente. Nota: puoi vedere solo i messaggi inviati nelle aree dove hai l'accesso.

Mostra messaggi Menu

Messaggi - Eutidemo

Pagine 1 ... 127 128 129 130 131 ... 410
#1921
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
02 Marzo 2023, 11:38:39 AM
Ciao Iano. :)
Innanzittutto grazie per gli immeritati ringraziamenti!
***
Sono contento che il mio avventurarmi per la prima volta in vita mia (in avanzata vecchiaia) alla scoperta della matematica, possa aiutarvi a rinnovare il vostro stupore verso le conquiste vecchie e nuove della matematica.
Peccato, però, che per me sia ormai troppo tardi; ed infatti, non ho più nè la capacità cerebrale nè l'elasticità mentale per comprendere certi concetti (che, in realtà, non ho mai avute neanche da giovane).
***
Un saluto! :)
***
#1922
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
02 Marzo 2023, 11:26:32 AM
Ciao Baylham. :)
Veramente anch'io, in una mia risposta a Phil, ero partito esattamente dalla tua stessa premessa; e, cioè, che bisogna partire dal fatto che, nella "realtà fisica", ogni "misurazione" è soltanto una "approssimazione".
Per cui, nella "realtà fisica", l'esistenza di quadrati perfetti o imperfetti in base al lato o all'area  non ha alcun senso.
***
Al riguardo, avevo testualmente precisato che "tutto ciò che è concretamente "reale" è anche naturalmente "approssimato"; questo è ovvio, perchè, nella "realtà fisica", non esistono "mai" forme geometriche dalle misure assolutamente "perfette" (siano esse cerchi, quadrati o triangoli)!"
***
Però, tu e Phil, dovreste concedermi che, nella "realtà matematica", ed anche in quella  "geometrica", il concetto di "approssimazione" è un po' diverso da quello di  "approssimazione" fisica; si tratta, cioè, di due tipi di "approssimazione" completamente differenti.
***
Ed infatti, nella "realtà matematica", ed anche in quella  "geometrica", esistono:
- delle figure dalle misure assolutamente "perfette";
- delle figure dalle misure "imperfette" (ovvero "approssimate", che dir si voglia).
***
Ad esempio, nella "realtà matematica", ed anche in quella  "geometrica":
.
a)
Un quadrato dall'area di 400,00 mq, la cui radice  quadrata è pari a 20,00 mt "esatti", ha un lato dalla "misura ben definita" di 20,00 mt; per cui, se moltiplichiamo aritmeticamente tale lato per sè stesso, otterremo un area  dall'area di 400,00 mq "esatti".
E lo stesso dicasi per il tuo esempio del quadrato con un lato di 5,00 mt "esatti". ; il quale avrà senz'altro un'area di 25 mq "esatti".
 .
b)
Un quadrato dall'area di 5024 mq (o di 1256 mq), invece, la cui radice  quadrata ci dà un "numero irrazionale", ha un lato dalla misura matematicamente "approssimata"; per cui, se moltiplichiamo aritmeticamente tale lato  "approssimato" per sè stesso, otterremo, sì, un quadrato dall'area di circa 5024 mq (o di 1256 mq), però matematicamente "approssimata".
.
***
Si badi: "matematicamente" e non "fisicamente"
***  
.
***
Non a caso, in matematica, esistono i simboli di:
- "uguale"
- "disuguale"
- "approssimativamente uguale"
***
Nonchè:
- Q per i numeri razionali;
- I per i numeri irrazionali.
***
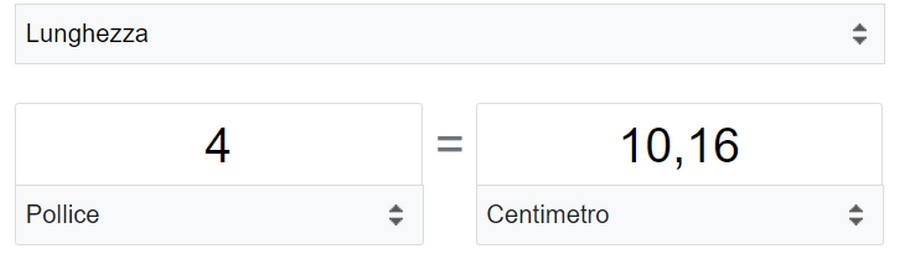
Di conseguenza, il mio "pseudo-teorema" ( ;D ) , grazie anche ai tuoi preziosi suggerimenti, andrebbe così corretto.
***
Così ti sembra che possa andare un po' meglio?
Grazie!
***
.
***
Un saluto! :)
***
#1923
Tematiche Spirituali / Re: La Bibbia e l'eutanasia
02 Marzo 2023, 06:42:06 AM
Ciao Taurus. :)
Bravo!
Mi ero dimenticato di citare anche il capitolo 4  del Qoélet; passo da te molto appropriatamente riportato, in quanto molto pertinente al mio TOPIC.
***
.
***
Passo che ricorda quello, molto simile, della "Nascita della tragedia" di Nietzsche:
«L'antica leggenda narra che il re Mida inseguì a lungo nella foresta il saggio Sileno, seguace di Dioniso, senza prenderlo. Quando quello gli cadde infine fra le mani, il re domandò quale fosse la cosa migliore e più desiderabile per l'uomo. Rigido e immobile, il demone tace; finché, costretto dal re, esce da ultimo tra stridule risa in queste parole: "Stirpe miserabile ed effimera, figlio del caso e della pena, perché mi costringi a dirti ciò che per te è vantaggiosissimo non sentire? Il meglio è per te assolutamente irraggiungibile: non essere nato, non essere, essere niente. Ma la cosa in secondo luogo migliore per te è - morire il prima possibile".»
.
***
Un saluto! :)
***
#1924
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
02 Marzo 2023, 06:26:40 AM
Ciao Iano. :)
Secondo me sei tu che confondi il "linguaggio comune" con il "linguaggio geometrico".
***
Ed infatti, "geometricamente":
.
a)
L'"estensione", indica in quante direzioni può essere "esteso" un oggetto nello spazio.
.
b)
La "lunghezza", invece, indica solo uno dei vari tipi di "estensione" che un oggetto  può avere nello spazio.
.
***
E' invece vero che, per "misurare" qualsiasi tipo di "estensione" di un oggetto (lunghezza compresa), servono almeno due "elementi" per fare un confronto:
- l'oggetto stesso;
- l'unità di misura prescelta.
Ma io non ho mai detto il contrario! ;)
.
***
Quanto al fatto che l'uomo non è "misura", bensì "misuratore" di tutte le cose, cioè colui che confronta gli oggetti, tale concetto era chiarissimo sia a Protagora, così come lo è al sottoscritto; ed infatti è ovvio che "misura" era ed è solo una "metafora" retorica per dire "misuratore".
Il fatto che io abbia portato l'esempio dei "pollici" (o anche dei "piedi"), era solo per mettere in rilievo la singolare circostanza, per la quale, sebbene l'uomo sia senz'altro il "misuratore" di tutte le cose, in alcune culture misura le cose facendo riferimento alle dimensioni (standardizzate) di parti del suo corpo.
Ma era solo una scherzosa osservazione etnologica, senza alcuna implicazione di carattere matematico, geometrico o filosofico!
***
.
***
Un saluto! :)
***
#1925
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
02 Marzo 2023, 05:31:02 AM
Ciao Phil. :)
Sono perfettamente d'accordo con te che tutto ciò che è "reale" è anche naturalmente "approssimato"; questo è ovvio, perchè, nella "realtà fisica", non esistono "mai" forme geometriche dalle misure assolutamente "perfette" (siano esse cerchi, quadrati o triangoli)!
***
Però dovresti concedermi che, nella "realtà matematica", ed anche in quella  "geometrica", il concetto di "approssimazione" è diverso da quello di  "approssimazione" fisica.
Ed infatti, nella "realtà matematica", ed anche in quella  "geometrica", esistono:
- delle figure dalle misure assolutamente "perfette";
- delle figure dalle misure "imperfette" (ovvero "approssimate", che dir si voglia).
***
Ad esempio, nella "realtà matematica", ed anche in quella  "geometrica":
a)
Un quadrato dall'area di 400,00 mq, la cui radice  quadrata è pari a 20,00 mt "esatti", ha un lato dalla "misura ben definita" di 20,00 mt; per cui, se moltiplichiamo aritmeticamente tale lato per sè stesso, otterremo un area  dall'area di 400,00 mq "esatti".
b)
Un quadrato dall'area di 5024 mq (o di 1256 mq), invece, la cui radice  quadrata ci dà un "numero irrazionale", ha un lato dalla misura soltanto "approssimata"; per cui, se moltiplichiamo aritmeticamente tale lato  "approssimato" per sè stesso, otterremo un quadrato dall'area di 5024 mq (o di 1256 mq), però soltanto "approssimata".
***
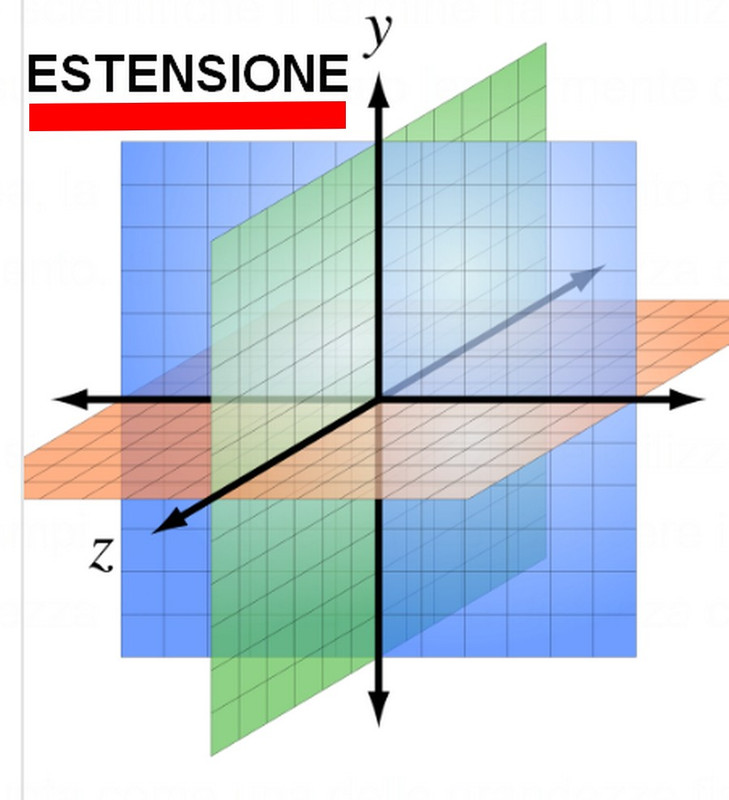
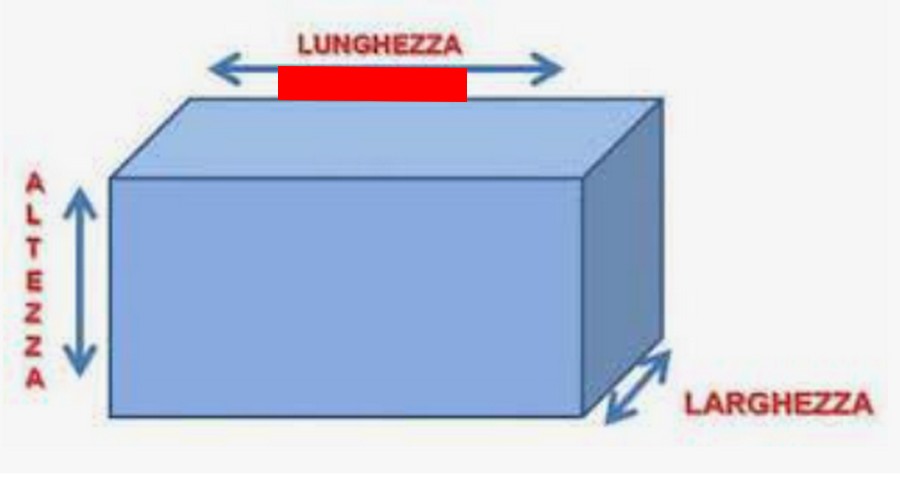
Alla stregua di quanto sopra, ti chiedo se, almeno secondo te, il mio "teorema" (si fa per dire, ovviamente, perchè io non sono certo all'altezza di poter enunciare teoremi :D ), dal punto di vista strettamente "matematico" e "geometrico", sia corretto o meno.
***
Un saluto! :)
***
#1926
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 17:11:26 PM
Ciao Phil. :)
Io non sono in grado di stabilire se sia più corretto il risultato ottenuto con la tua calcolatrice o con quella di Baylham, però, secondo me:
1)
Se è più corretto il risultato ottenuto con la tua calcolatrice, il mio "teorema" (si fa per dire) non ha alcun fondamento, poichè parte da premesse errate.
2)
Se, invece, è più corretto il risultato ottenuto con la calcolatrice di Baylham, il mio "teorema" (si fa per dire) potrebbe avere fondamento, poichè parte da premesse corrette.
***
Ed infatti Baylham ha scritto: "A giudicare dai numeri calcolati dall'elaboratore, le radici quadrate di 5024 e 1256 sono numeri irrazionali; i cui risultati sono quindi solo delle approssimazioni."
Ma se le radici quadrate dei lotti catastali quadrati di 5024 mq e di 1256 mq, come lui sostiene, sono "numeri irrazionali", ciò vuol dire che anche le aree di alcuni quadrati sono il prodotto di "numeri irrazionali" moltiplicati tra di loro (lato per lato), e, quindi, sono necessariamente approssimate.
***
Se così fosse il mio "teorema" potrebbe essere valido!
***
Ed infatti:
- se il risultato della radice quadrata della presunta area catastale di un quadrato, moltiplicato per se stesso, non corrisponde in modo preciso all'area dal quale è stato "eradicato", ciò vuol dire che un quadrato "esattamente" di quell'area non può esistere;
- se, invece, il risultato della radice quadrata della presunta area catastale di un quadrato (magari di 400 mq), moltiplicato per se stesso, corrisponde in modo preciso all'area dal quale è stato "eradicato", ciò vuol dire che un quadrato "esattamente" di quell'area può geometricamente e matematicamente esistere.
***
Un saluto! :)
***
#1927
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 16:54:50 PM
Citazione di: iano il 01 Marzo 2023, 13:55:01 PMCi sta o non ci sta? :)
Ci sta! ;)
#1928
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 16:49:59 PM
Ciao Iano :)
Quando ho fatto riferimento a Protagora, il quale diceva che "L'uomo è misura di tutte le cose", l'ho fatto a ragione veduta; ed infatti, per millenni, ed anche oggi, l'uomo è "misura" di tutte le cose non solo sotto il profilo "filosofico", ma anche sotto il profilo meramente "fisico".
Almeno utilizzando "pezzi di uomo"!
***
Ad esempio, la "misura" della canna di questo mio revolver, è di circa "QUATTRO POLLICI".
***
Ma, come "misura", possiamo prendere anche quella "metrica"; nel qual caso la canna di questo mio revolver, è circa di "DIECI CENTIMETRI".
***
E' chiaro, infatti, che le "unità di misura" sono "convenzionali"; ciò in quanto la "misura" è il valore numerico pari al rapporto tra una grandezza e un'altra ad essa omogenea, assunta "convenzionalmente" come unità.
***
Per cui, se diciamo di ''misurare qualcosa'', non partiamo affatto "col piede sbagliato";  purchè, però, precisiamo quale sia l'unità di misura a cui facciamo riferimento.
***
E, comunque, così come ogni lingua può essere tradotta in un'altra, così ogni unità di misura può essere tradotta in un'altra.
***
In genere, comunque, quasi tutte le cose sono fra loro commensurabili; ed infatti è molto difficile che ci si metta a discutere circa l'effettiva lunghezza di un oggetto rispetto all'altro, perchè la cosa è facilmente verificabile in modo oggettivo (qualsiasi unità di misura si utilizzi).
Salvo determinati casi, ovviamente!
:D :D :D :D :D :D :D :D :D :D :D :D :D 
***
Quanto ai "quanti", se mi consenti il "calembour", io non farei confusione tra la "macrofisica" e la "microfisica"; perchè seguono leggi molto diverse!
***
Un saluto! :)
***
#1929
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 13:36:14 PM
Ciao Iano. :)
Tu scrivi che dire che il cerchio non è "quadrabile" equivale a dire che il quadrato non è "cerchiabile"; il che ci può anche stare!
***
Però, secondo me:
a)
Un quadrato di 20 metri di lato, ha un area di 400 metri quadrati "esatti" (ottenuta calcolando "numeri razionali").
b)
Un cerchio con raggio di 20 mt, invece, ha un'area di 1.256 mq "approssimati" (ottenuta calcolando "numeri irrazionali").
***
Non si tratta di assumere la "misura" come un "assioma", bensì come il risultato di un diverso tipo di calcolo.
***
Sono invece d'accordo con il famoso motto di Protagora: " άνθρωπος είναι το μέτρο των πάντων»  ("L'uomo è misura  di tutte le cose") (Protagora, fr.1, in Platone, Teeteto, 152a)
***
Un saluto! :)
***
#1930
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 13:16:58 PM
Ciao Phil. :)
Tu dici che Baylham ha ragione.
Però:
.
1)
Tu hai scritto che i risultati esatti e completi delle radici quadrate del lotto completo e di quello quadripartito erano:
a)
70,880180586677401607964500390145 metri, che elevato al quadrato dà senza arrotondare i 5024 metri quadri di partenza.
b)
35,440090293338700803982250195073 metri per lato, che elevato al quadrato dà senza arrotondare esattamente 1256 metri quadrati per ogni sotto-quadrato.
.
2)
Baylham, invece, ha scritto "A giudicare dai numeri calcolati dall'elaboratore, le radici quadrate di 5024 e 1256 sono numeri irrazionali; i risultati sono quindi solo delle approssimazioni."
.
***
Mi sembra, quindi, che i risultati dei vostri elaboratori non coincidano, o sbaglio?
***
.
***
Per il resto, invece, sebbene dal basso della mia nescienza, penso di poter essere d'accordo con te sul fatto che cerchi con ugual raggio, avranno uguale area; ma allora non si può dire anche che sfere dello stesso raggio avranno lo stesso volume?
***
Un saluto! :)
***
#1931
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 13:03:20 PM
Citazione di: atomista non pentito il 01 Marzo 2023, 10:37:01 AMEcco , mi e' tornato il mal di testa :)
Ti capisco perfettamente! :(
Io sto perdendo il bandolo ::)
#1932
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 13:01:09 PM
Ciao Baylham.
Tu scrivi: "A giudicare dai numeri calcolati dall'elaboratore, le radici quadrate di 5024 e 1256 sono numeri irrazionali; i risultati sono quindi solo delle approssimazioni."
Ma se le radici quadrate dei lotti catastali quadrati di 5024 mq e di 1256 mq, come tu sostieni, sono "numeri irrazionali", ciò vuol dire che anche le aree di alcuni quadrati sono il prodotto di "numeri irrazionali" moltiplicati tra di loro (lato per lato), e, quindi, necessariamente approssimate?
Se così fosse il mio "teorema" sarebbe valido!
***
Ed infatti, se il risultato della radice quadrata della presunta area catastale di un quadrato, moltiplicato per se stesso, non corrisponde all'area dal quale è stato "eradicato", ciò vuol dire che un quadrato "esattamente" di quell'area non può esistere.
***
Oppure, come è molto probabile, c'è qualcosa che "non quadra" nel mio ragionamento? ::)
***
Ed infatti, secondo te, è mai possibile che il lato di un quadrato sia misurabile solo per "approssimazione", e che la sua lunghezza sia costituita da un numero "irrazionale"?
Ma se la cosa non fosse possibile, allora non dovrebbe essere possibile neanche che esistano lotti catastali quadrati di 5024 mq e di 1256 mq, le cui radici quadrate, come tu sostieni, sono "numeri irrazionali".
***
Basta, sto davvero cominciando a "dare i numeri"; perdonatemi!
***
Un saluto! :)
***
P.S.
Mi sembra, però, che i risultati della tua calcolatrice non concordino con quella di Phil!
#1933
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 06:31:06 AM
Ciao Iano :)
Concordo con te che, laddove una figura geometrica, come il cerchio, non sia esattamente misurabile, dobbiamo rassegnarci alle approssimazioni; altrimenti cadremmo nel "nichilismo" (se non altro sotto il profilo operativo).
Un saluto! :)
#1934
Tematiche Filosofiche / Re: Il teorema di Eutidemo :-D
01 Marzo 2023, 06:22:17 AM
Ciao Phil :)
Beato te a cui basta "ripassare" un po' la matematica; io, invece, prima di parlarne a sproposito, dovrei "ristudiarla ex novo", in quanto al liceo classico, ne ho fatta poca e male (e molto tempo fa).
Senza contare che il mio Q.I. "matematico" è inferiore al mio Q.I. "linguistico" e "spaziale".
***
Per cui, visto che tu, in materia, ne sai (e ne capisci) molto più di me, vorrei farti due domande, per curiosità personale:
.
1)
Invece di dire che la "quadratura del cerchio" è "impossibile" (come effettivamente è), non sarebbe più semplice dire :
a)
Che l'area del  cerchio non è mai esattamente "misurabile", a causa del  𝝅 (3,14), i cui decimali sono pressochè infiniti e/o indefiniti:
https://it.wikipedia.org/wiki/Prime_100000_cifre_di_Pi_greco
b)
Per cui, visto che l'area del  cerchio non è "mai" esattamante "misurabile", di conseguenza è "impossibile" equipararla a nessuna altra forma geometrica esattamente "misurabile"; il che, per una questione di mera "logica", oltre che di "matematica".
Cioè, invece di dire che la "quadratura del cerchio" è "impossibile", perchè non dire che è "impossibile" anche la "triangolatura", la "rettangolatura", la "pentagonatura" del cerchio, e via dicendo?
Oppure queste sono invece possibili (confesso la mia ignoranza in materia)?
Inoltre, se è vero che l'area del  cerchio non è "mai" esattamante "misurabile", di conseguenza dovrebbe essere "impossibile" equipararla esattamente neanche all'area di un qualsiasi altro cerchio; perchè, se nessun cerchio è "mai" esattamante "misurabile", come si fa a dire che è "esattamente identico" ad un altro cerchio?
E' "esattamente identico" solo se ci si ferma agli stessi decimali (il secondo o il centomilessimo), ignorando quelli che vengono dopo.
.
2)
La circostanza che la "quadratura del cerchio" sia "impossibile" comporta che anche la "cubatura" della "sfera" sia parimenti impossibile?
Ovvero che il volume della sfera sia anch'esso "non misurabile" in alcun modo preciso?
Penso, nella mia nescienza, che dovrebbe essere così, perchè nella formula del calcolo del volume della sfera c'è sempre di mezzo il "π": V = 4/3πr. raggio.
Però, immergendo una sfera materiale in un contenitore graduato, il suo volume può conoscersi "esattamente" (almeno sotto il profilo "fisico") trasformandola in "parallelepipedo rettangolo"; il quale, in determinati casi, potrebbe essere anche un "cubo".
Il che, ovviamente, tenendo conto dei principi della fisica che regolano il comportamento dei solidi immersi in un liquido; e che, comunque, la "fisica", anche se è strettamente collegata alla "matematica", è una cosa alquanto diversa, essendo "concreta" e non "astratta".
***
Un saluto! :)
***
P.S.
Se le mie domande sono troppo stupide, sei esonerato dal rispondere!
#1935
Storia / Re: Una strana preistoria
28 Febbraio 2023, 17:22:09 PM
Citazione di: Pensarbene il 25 Febbraio 2023, 06:15:54 AMPremetto che non voglio parlare di ufo e alieni ma proporre una disamina pacata su alcuni aspetti della preistoria umana.

Uno dei miei interessi è lo studio della preistoria umana basato su ciò che abbiamo di reale e concreto di essa
In pratica, petroglifi, graffiti, pitture nelle grotte e su rocce.
Studiando questi reperti, sono rimasto sorpreso da un fatto curioso e interessante: molte di queste opere appaiono nello stesso periodo di tempo in aree del pianeta diverse e lontane tra di loro:

https://it.m.wikipedia.org/wiki/Incisioni_rupestri

Leggendo attentamente l'articolo che vi ho proposto, vi siete resi conto della somiglianza di molti graffiti e pitture rupestri.Questa somiglianza indica qualcosa di interessante che, a quanto ne so, non ha avuto una spiegazione seria e rigorosa.
Come mai uomini preistorici, abitanti in aree diverse e lontane del pianeta, in epoche simili, hanno segnato rocce e grotte con graffiti e pitture simili, a volte quasi uguali?
Una prima risposta potrebbe essere questa: esiste un inconscio collettivo negli esseri umani che si esprime in modo simbolico.
Così, i personaggi raffigurati, alcuni animali particolari, segni e graffi, indicherebbero il passaggio dell'uomo da una primitività istintuale e grezza ad una più mediata e umanizzata.
In particolare, segnalerebbero l'avvento del linguaggio attraverso il simbolismo.
Non trovo altre spiegazioni anche perché trovo molto improbabile che questa primitiva "cultura" possa essere stata frutto di migrazioni e contatti di genti di aree così diverse e lontane tra di loro.
Inoltre, troviamo gli stessi simboli e creazioni nel continente americano e perfino in Australia, quindi l'ipotesi del contatto tra popoli mi sembra molto improbabile se non impossibile.
Facendo un parallelo con  la storia della cultura e dell'arte,posso notare l'apparizione di idee, creazioni artistiche e movimenti culturali simili in aree diverse del pianeta più o meno nello stesso periodo di tempo.
Questo, in un modo meno eclatante di quello preistorico ma pur sempre interessante e sorprendente.
È probabile che la specie si sviluppi e evolva seguendo linee e direttrici caratteristiche della specie stessa, producendo similmente e sincronicamente?
Il DNA umano potrebbe essere sequenziale e sequenziato non soltanto nel suo modo di funzionare
naturale ma anche per quanto riguarda il linguaggio,il simbolismo,la creatività?



In realtà in nostri antenati si sono sparsi in tutto il mondo, partendo da un'area limitata dell'Africa Orientale; per cui non è assurdo ipotizzare che, da lì, ogni gruppo migratorio si sia portato dietro almeno parte degli archetipi che avevano tutti originariamente in comune!
Pagine 1 ... 127 128 129 130 131 ... 410