Ciao Phil. 
Hai capito esattamente il senso del mio dialogo; sono io che sono stato "tradito" dalla "calcolatrice online" che ho utilizzato, la quale, come risultato delle radici quadrate, mi ha dato:
a)
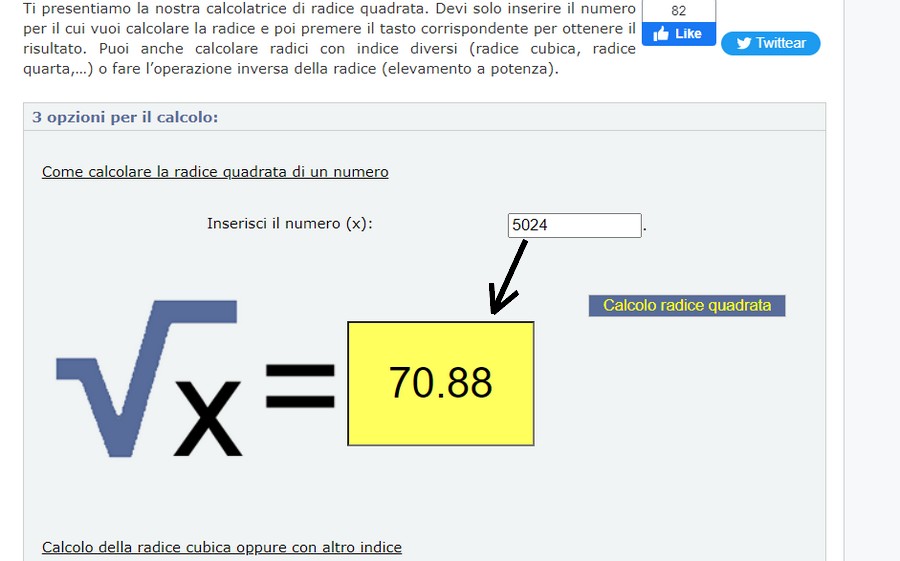
70,88 mt lineari secchi, senza ulteriori decimali.
b)
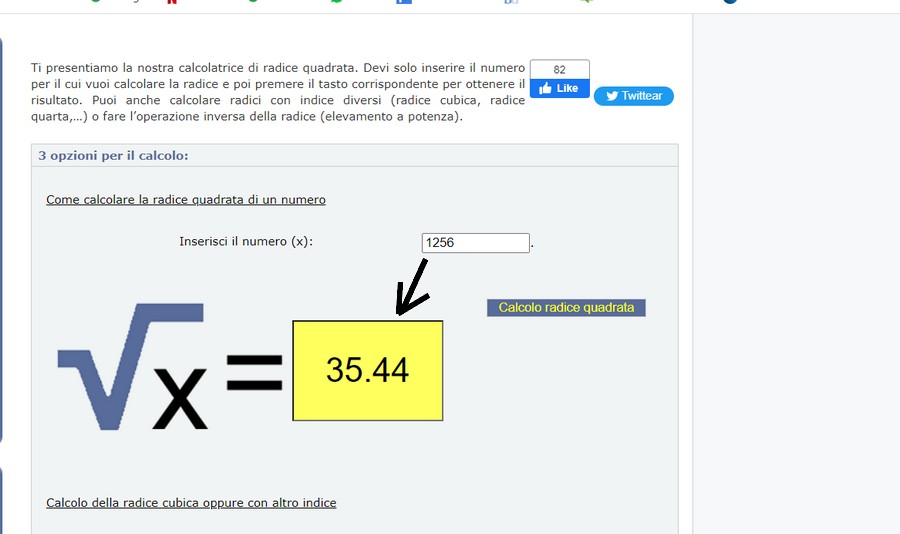
35,44 mt lineari secchi, senza ulteriori decimali.
***
Di qui scaturivano tutti i miei seguenti calcoli, ragionamenti e "teoremi", perchè la "calcolatrice online" non mi aveva fornito tutti i decimali delle due radici quadrate; almeno avrebbero potuto precisare che, per ragioni di spazio, si limitavano soltanto ai primi due.
Invece non l'hanno fatto, traendomi così in inganno. 
***
Ed invece, come da te correttamente riportato, i risultati esatti e completi delle radici quadrate erano:
a)
70,880180586677401607964500390145 metri (che elevato al quadrato dà senza arrotondare i 5024 metri quadri di partenza)
b)
35,440090293338700803982250195073 metri per lato (che elevato al quadrato dà senza arrotondare esattamente 1256 metri quadrati per ogni sotto-quadrato).
***
Per cui, partendo da dati numerici incompleti, quali quelli fornitimi dalla dalla "calcolatrice online" che avevo utilizzato, tutto il mio conseguente ragionamento deve considerarsi fallace, in quanto fondato su premesse erronee; anche se, in questo caso, credo non per mia colpa. 
***
Ti chiedo comunque scusa per il tempo inutile che ti ho fatto perdere, e ti ringrazio per le tue precisazioni.
***
Un saluto.
***
(P.S. Dove diamine la trovo online una calcolatrice che mi dia tutti i decimali completi di una operazione?)
), ed è stato fotografato più volte con lui, come nella seguente foto; la quale è ufficiale, in quanto scattata nel contesto delle celebrazioni del giorno dei "padri della patria", in qualità di assegnatario di ben "quattro decorazioni militari", appuntatagli sul petto dal Putin. 
