Ciao Iano.

Hai ragione, in quanto, tecnicamente,  non si tratta di una vera e propria "reductio ad absurdum"; ed infatti, come giustamente osservi tu, nelle dimostrazioni per assurdo si dimostra la falsità dell'assunto a partire dagli assiomi.

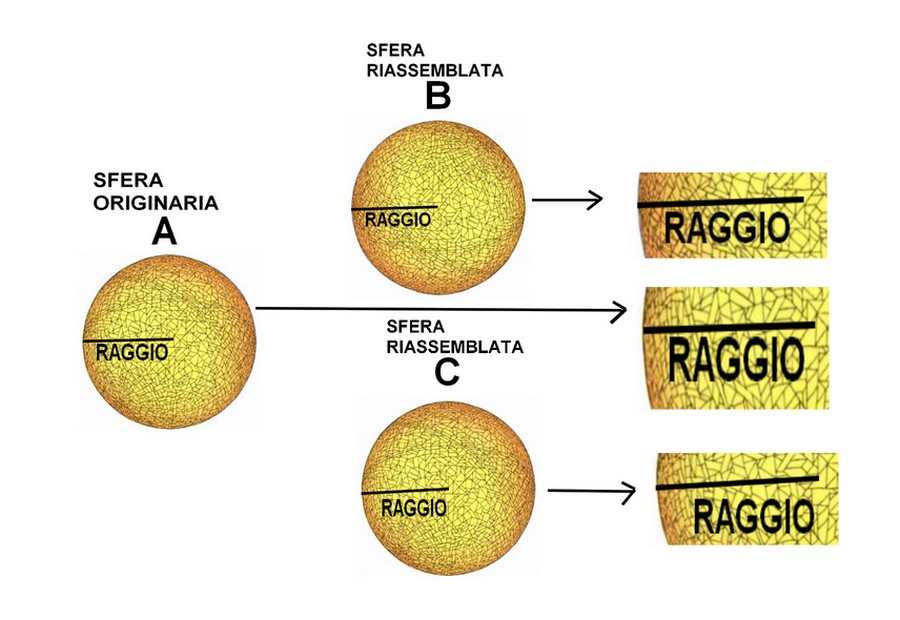
Io ho utilizzato tale espressione in modo "impropriamente esteso", nel senso, cioè, che, se lo scopo di Hausdorff-Banach-Tarski era quello di "dimostrare" che, se da un teorema matematicamente "dimostrato" si può ricavare un "paradosso" come quello del "raddoppio della sfera", allora vuol dire che sono gli "assiomi" a partire dai quali si è dimostrato tale teorema ad essere ''errati".

Un saluto!

***
P.S.
Tieni conto delle mie "virgolette", sebbene io abbia il vizio di usarne un po' troppe (e spesso anche a sproposito).

Ciao Socrate 78

La somministrazione di morfina è in proporzione "diretta" o "inversa" alla intensità del dolore.

Ed infatti, dopo l'intervento di "ricostruzione cranica", mi misero in mano una "pompa di morfina", affinchè io stesso ne regolassi da solo il flusso a seconda della intensità del dolore che provavo; flusso che io diminuii poco a poco, mano a mano che il dolore al cuoio capelluto diminuiva.

Nel caso di malati terminali di cancro, poichè in fase terminale il dolore aumenta progressivamente, il personale sanitario aumenta progressivamente anche la dose di morfina, per attenuarlo in modo accettabile; altrimenti, se, ad un certo punto, smettessero di aumentare la dose di morfina per evitare il rischio di depressione cerebrale e respiratoria, l'unico risultato che otterrebbero sarebbe quello di vedere il malato contorcersi nel suo giaciglio a causa di sofferenze sempre più strazianti e lancinanti.

Per poi morire comunque, magari poco tempo dopo, a causa del dolore invece che della morfina!

Lo scopo della medicina è quello di farci "vivere più a lungo" (e bene), ma non è certo quello di farci "morire più lentamente" (e male).

Un saluto!

Ciao Bobmax.

Sono d'accordo con te!

Ma la dimostrazione del "paradosso" del raddoppiamento della della sfera:
-non solo conferma l'assurdità della pretesa di giocare con "insiemi infiniti";
- ma anche la pretesa di giocare con "insiemi finiti" composti da "elementi non misurabili".
Secondo me se tratta "quasi" di una "contradictio in adjecto".

Ed infatti, se io possiedo un "insieme finito" di libri, posso misurare:

- sia la "lunghezza" dell'intero insieme mettendoli tutti in fila (in metri);

- sia il "peso" dell'intero insieme mettendoli tutti su una bilancia (in chilogrammi).

Ma se io possiedo un "insieme finito" di "elementi non misurabili", come faccio a misurare il loro "insieme", che, pure, è "finito" (e cioè "misurabile")?

Un saluto!

Ciao Iano.

Il "Teorema di Pitagora" dimostra teoricamente che in ogni triangolo rettangolo l'area del quadrato costruito sull'ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti; ed infatti, se io disegno "materialmente" un triangolo rettangolo, e poi misuro l'area del quadrato costruito sull'ipotenusa, nonchè  le aree dei quadrati costruiti sui cateti, posso materialmente constatare che la prima è esattamente identica alla somma delle aree dei quadrati costruiti sui secondi.

Quando Hausdorff-Banach-Tarski, dopo avermi rivelato "il numero esatto dei pezzi non misurabili utilizzati" (visto che si tratta, secondo loro, di un "insieme finito"), riusciranno a scomporre materialmente una sfera del raggio di un metro, per ricomporne  due che abbiano lo stesso raggio, allora darò loro ragione; altrimenti, per me, le loro formule matematiche non costituiscono nessun dimostrabile "Teorema", ma solo un "Sofisma" matematico.

Ma se lo scopo di Hausdorff-Banach-Tarski era invece quello di "dimostrare" che, se da un teorema matematicamente "dimostrato" si può ricavare un "paradosso" come quello del "raddoppio della sfera", allora vuol dire che sono gli "assiomi" a partire dai quali si è dimostrato tale teorema ad essere ''errati", allora io sono perfettamente d'accordo con loro.
***
Per cui, se dall'''assioma di scelta'' formulato da Ernst Zermelo nel 1904 (secondo il quale dato un insieme "I", non vuoto, -aggregato di insiemi- i cui elementi sono a lor volta insiemi non vuoti, è possibile scegliere un elemento per ogni insieme e considerarlo come un rappresentante dell'insieme stesso e costruire con questi rappresentanti un nuovo insieme "II", da sostituire ad "I"), deriva consequenzialmente uno "pseudo paradosso" come quello del "raddoppio della sfera", allora, evidentemente, l'''assioma di scelta'' è errato.
E lo "pseudo paradosso" del "raddoppio della sfera" non è altro che una "demonstratio ex absurdo" da parte di Hausdorff-Banach-Tarski  per dimostrare la fallacità di tale assunto!
***
Un saluto!
***
P.S.
Ringrazio Iano per il riferimento all'''assioma di scelta'' formulato da Ernst Zermelo, che io, invece, avevo colpevolmente trascurato.

Ciao Phil.

E' vero, le tue statistiche sono molto più confortanti delle mie; ed anche se non possono essere "paragonate" tra di loro, tuttavia, come ho scritto, "confrontate" l'una con l'altra, esse potrebbero suggerirci interessanti ipotesi circa le diversità "caratteriali" e "comportamentali" delle differenti popolazioni considerate.

E, tutto sommato, noi Italiani non ne usciremmo poi troppo male; anche considerato l'elevato numero di omicidi di natura accidentale, dovuto all'improprio uso di armi semiautomatiche.

Il che costituiva l'oggetto specifico del mio topic.

Un saluto!

Il "paradosso" di Hausdorff-Banach-Tarski, noto anche come il "raddoppiamento della sfera", sostiene che è possibile prendere una "sfera nello spazio a tre dimensioni", suddividerla in un "insieme finito" di "pezzi non misurabili" e, utilizzando solo "rotazioni" e "traslazioni", riassemblare i pezzi in modo da ottenere due sfere dello "stesso raggio" (misurabile) della sfera originale.

.

Riguardo alla terminologia usata da Hausdorff-Banach-Tarski, rileviamo quanto segue:
.

Il volume di una sfera nello spazio a tre dimensioni si calcola moltiplicando per 4 il prodotto tra π (3,14) e il cubo del raggio, e poi dividendo il prodotto per 3 (V=(4πr3)/3).

Cioè, se una sfera ha il raggio della "misura" di 2 metri, il suo cubo sarà di 8 metri; per cui 3,14 x 8 = 25,12 x 4 = 100,48 : 3 = 33,49.

Il che presuppone necessariamente che il raggio della sfera sia "misurabile"!

.
b)

Detto in "matematichese", un insieme è detto "finito" se esiste una corrispondenza biunivoca (ossia una "biiezione") tra un numero naturale "n" visto come insieme e X.

Detto in italiano, e non in "matematichese", un insieme è finito se è composto da un numero finito di elementi; ad esempio, l'insieme dei libri della mia biblioteca.

Il che mi sembra un modo molto più semplice e comprensibile di esprimere il concetto.
.

Le grandezze misurabili sono sei: lunghezza, massa, tempo, intensità di corrente elettrica, temperatura e quantità di materia.

Altre caratteristiche, invece, non sono "misurabili"; ad esempio, la dimensione di un pallone è misurabile, mentre non è misurabile il suo colore.

Il concetto di "pezzi non misurabili", quindi, come vedremo più avanti, è molto ambiguo.
.

La "rotazione" è il movimento di un corpo che segue una traiettoria circolare:

- in due dimensioni, cioè sul piano, una figura può ruotare attorno ad un punto detto centro di istantanea rotazione;

- in tre dimensioni, la rotazione avviene intorno ad una retta detta asse di istantanea rotazione e più in generale, una rotazione in n dimensioni avviene attorno ad uno spazio a (n-2) dimensioni.

Per cui, ad esempio, un punto non può ruotare su se stesso.
.

La "traslazione" è una trasformazione affine dello spazio euclideo, che sposta tutti i punti di una distanza fissa nella stessa direzione.

.

Ciò premesso osservo quanto segue:

.

Per "pezzi non misurabili" si possono intendere cose diverse, e cioè:
.

"Pezzi solidi irregolari", quali entità non tipiche, come un "masso" o qualsiasi altro "oggetto informe", in quanto non possiedono nessuna qualità tipica che li renda misurabili in modo universale ed oggettivo; ad esempio come si fa per un cubo, elevando al "cubo" (alla terza potenza) la lunghezza del lato di uno qualsiasi dei quadrati che formano le sue facciate.

Per la determinazione del volume preciso di un "solido irregolare", invece, non si utilizzano formule fisse, ma si ricorre ad una "misurazione indiretta".

Cioè, ci si procura, cioè, un contenitore graduato, si aggiunge dell'acqua per metà, senza riempire il recipiente, e si segna l'esatto livello dell'acqua;  dopo di che, si immerge il "corpo irregolare", ad esempio una pietra o un pezzo informe di una sfera, nell'acqua del recipiente e si misura di quanto aumenta il livello dell'acqua.

In tal modo si può calcolare per differenza lo spazio occupato dal solido irregolare, cioè "misurare" il suo volume;  ovviamente tenendo conto dei principi della fisica che regolano il comportamento dei solidi immersi in un liquido.

Ma in tal modo il paradosso di Hausdorff-Banach-Tarski "non funzionerebbe", perchè, sia pure indirettamente, i "pezzi" in cui si scompone la sfera originaria, qualunque forma irregolare abbiano, sono comunque "misurabili".
.

Ed invece, almeno per quello che ho capito io, i "pezzi non misurabili" di cui al paradosso di Hausdorff-Banach-Tarski, non devono essere misurabili:

- nè "direttamente";

- nè "indirettamente".

Ma allora, essendo "privi volume" e di "dimensione", si potrebbe concludere che i "pezzi non misurabili" di cui al paradosso di Hausdorff-Banach-Tarski siano i "punti" di cui è composta la sfera.

Ma questo andrebbe contro il postulato del paradosso, che considera una sfera costituita da un "insieme finito" di "pezzi non misurabili";  per cui, se noi considerassimo come "pezzi non misurabili" i semplici "punti" di cui è composta la sfera, avremmo una sfera costituita da un "insieme infinito" ( e non "finito") di "pezzi non misurabili".

Perchè qualsiasi sfera, a prescindere dalla sua dimensione, è costituita da un "insieme infinito" di punti.
.

Inoltre, poichè i "pezzi non misurabili" in questione possono subire una "rotazione", la quale non può che avvenire  intorno ad una retta detta asse di rotazione, è evidente che, qualunque cosa essi siano, i "pezzi non misurabili" di Hausdorff-Banach-Tarski  non possono essere dei semplici "punti"; ed infatti nessun punto può essere ruotato su se stesso.
.

Infine, se la "sfera nello spazio a tre dimensioni" di Hausdorff-Banach-Tarski  è un "insieme finito" di "pezzi non misurabili", così come così lo è l'insieme dei libri della mia biblioteca, mettendo da parte il mistero di "che cosa" sono i "pezzi non misurabili",  Hausdorff-Banach-Tarski  dovrebbero essere in grado di dirci "quanti" sono tali pezzi; facendo, cioè, un esempio matematico e geometrico "concreto" del raddoppiamento di una qualsiasi sfera.

Ed infatti, un "insieme finito" di "pezzi", implica che se ne debba poter indicare il numero specifico; altrimenti non sarebbe un  "insieme finito", bensì un "insieme infinito" di pezzi.

.

Hausdorff-Banach-Tarski sostengono di poter riassemblare i "pezzi non misurabili" della sfera originaria, in modo da ottenere due sfere dello stesso "raggio" della sfera originale, utilizzando "rotazioni" e "traslazioni" particolari di tali "pezzi non misurabili"; cioè, come se si trattasse di "puzzle" tridimensionali, la cui miracolosa "ricomposizione" riuscirebbe a "raddoppiare" la singola sfera originaria.

Vale a dire, qualcosa del genere:

Però questo, secondo me, comporta degli ostacoli logici.
.

Dire di poter "ottenere due sfere dello stesso <<raggio>> della sfera originale", significa ammettere che tali "raggi" sono costituiti da segmenti di retta misurabili; altrimenti, se non li si possono misurare, come si fa a dire che sono "uguali"?
.

Ma come è possibile sostenere che i segmenti di retta che costituiscono i raggi delle due nuove sfere, ed il segmento di retta che costituisce il raggio della sfera originale sono "segmenti di retta misurabili" ed uguali, visto che sono costituiti da "frazioni di segmenti di retta non misurabili", in quanto attraversano "pezzi non misurabili"?

.
c)

Al che si potrebbe eccepire che i segmenti di retta che costituiscono i raggi delle due nuove sfere, ed il segmento di retta che costituisce il raggio della sfera originale sono "segmenti di retta misurabili", in quanto attraversano, sì, "pezzi non misurabili", ma il cui "spessore" traversato dal raggio delle sfere, è invece "misurabile".

Hausdorff-Banach-Tarski, però, parlano soltanto di "pezzi non misurabili", e non di "pezzi non misurabili dallo spessore misurabile"; ammesso che tale locuzione abbia molto senso.

Inoltre, in tal caso, si ricadrebbe nella fattispecie dei "solidi irregolari", da me esaminato sub 1) a).
.

Inoltre, se tali "puzzle" fossero realizzabili, si dovrebbe riuscire a realizzarli anche fisicamente, e non solo attraverso formule matematiche; ma, a quanto mi risulta, a fare una cosa del genere c'è riuscito solo Gesù Cristo, moltiplicando pani e pesci interi.

.

                                          CONCLUSIONE

Per concludere, secondo me, sia in pratica che in teoria, da una sfera di un metro di raggio, si potranno ricavare due sfere entrambe di uno stesso metro di raggio, soltanto in un modo:

- usando un palloncino atmosferico di un metro di raggio a pressione singola;

- rigonfiando i due palloncini a pressione doppia (sempre che si abbia a disposizione un materiale molto resistente, elastico ed espansibile).

Ciao InVerno.

La tua è stata un'analisi di "altissimo livello", sufficientemente "distaccata", "coinvolta", e "coinvolgente" nello stesso tempo; quindi, per quello che possono valere, meriti le mie più sentite congratulazioni!

Resta soltanto da vedere se siamo vicini al "punto di non ritorno":

Oppure se siamo già su un "piano inclinato":

Un saluto!

Secondo me non c'è assolutamente niente di "ideologico" nel condannare l'aggressione militare di una nazione ad un'altra; sarebbe come voler considerare "ideologica" la condanna di uno stupratore, in quanto lo stupro si ritiene giustificato dagli abiti provocanti della vittima

Semmai è "ideologico" voler considerare "ideologica" la condanna dell'aggressione russa; la quale, invece, è stata "legalmente" e "giuridicamente" pronunciata, alla quasi unanimità, dalla Corte Internazionale di Giustizia, composta da tredici giudici indipendenti (tra i quali anche uno russo, il quale, però, saggiamente, ha votato contro onde evitare di essere avvelenato da Putin).

Ciao Phil.

Non hai nessuna colpa, nè metto in dubbio l'affidabilità delle tue tabelle statistiche; però si tratta di rilevazioni statistiche diverse da quelle che avevo riportato io nel mio topic iniziale:

Le "statistiche" che avevo riportato io, nella quale noi Italiani siamo al secondo posto in classifica (dopo gli USA), riguardavano, infatti, in percentuale alla popolazione delle varie nazioni (per 100.000 abitanti):

- esclusivamente gli "omicidi" ("murder") commessi con le sole "armi da fuoco";

- sia "intenzionali", sia "colposi", sia "accidentali".

Ed invece:

a)

La tua prima tabella statistica riguarda, in percentuale alla popolazione delle varie nazioni (per 100.000 abitanti):

- sia gli "omicidi" sia i "suicidi" ("total deaths") commessi con le sole "armi da fuoco";

- sia "intenzionali", sia "colposi", sia "accidentali".

.
b)

La tua seconda tabella statistica riguarda, in percentuale alla popolazione delle varie nazioni (per 100.000 abitanti):

- esclusivamente gli "omicidi" ("homicide") commessi, però, con "qualsiasi mezzo", e non solo quelli commessi  con le "armi da fuoco";

- esclusivamente quelli "intenzionali", e non quelli "colposi" o "accidentali".

Per cui si tratta di tabelle che riguardano "tre" diverse "platee statistiche", le quali, quindi, essendo estrapolate da dati non omogenei, non possono essere "paragonate" tra di loro; ciò non toglie, però, che "confrontate" l'una con l'altra, esse potrebbero suggerirci interessanti ipotesi circa le diversità "caratteriali" e "comportamentali" delle differenti popolazioni considerate.

Ma questo è un compito troppo arduo, perchè io me la senta di affrontarlo; nè in questa sede nè in altro apposito topic.

Un saluto!

Ciao Phil e Jacopus.

Credo che abbia ragione Jacopus quando osserva che le varie statistiche, considerando aspetti diversi del fenomeno, non sono affatto in contraddizione tra di loro.

Ed infatti:
.

La "statistica" che ho riportato io, nella quale noi Italiani siamo al secondo posto in classifica (dopo gli USA), riguarda:

- "esclusivamente" gli omicidi commessi con le armi da fuoco;

- sia intenzionali, sia colposi, sia accidentali;

- in percentuale alla popolazione delle varie nazioni (per 100.000 abitanti).

.
b)

La "statistica" che ha riportato Phil, invece, riguarda:

- "complessivamente" tutti i i tipi di omicidio commessi in un determinato Paese, sia con armi da fuoco, sia con armi bianche sia a mani nude;

- però "esclusivamente" quelli intenzionali;

- in percentuale alla popolazione delle varie nazioni (per 100.000 abitanti).

.
c)

La "mappa" che ha riportato Phil, invece,  a differenza delle due precedenti statistiche, che consideravano solo gli  "omicidi", riguarda tutti i tipi di "morti per arma da fuoco"; compresi, quindi, anche i "suicidi".

Tanto è vero che, come si rileva da tale mappa, la Groenlandia, nazione con pochissimi "omicidi", surclassa però gli USA quanto  morti per "arma da fuoco" in generale; ed infatti la Groenlandia, "succursale" della Danimarca, vanta da decenni una percentuale di "suicidi" tra le più alte al mondo, che compensa lo scarso numero di "omicidi" nel novero generico delle "morti per arma da fuoco"

Un saluto ad entrambi!

In un mio recente topic, avevo aspramente criticato gli USA, per le stragi che laggiù si verificano continuamente con le armi da fuoco; poi, però, mi è venuto lo scrupolo di verificare come stanno le cose da noi.

Ero infatti convinto che l'Italia fosse agli ultimi posti nel mondo quanto agli omicidi commessi con pistole e fucili; ed infatti, a differenza di quasi tutti gli altri Paesi del mondo, a cominciare dagli USA, da noi, per fortuna, è rigorosamente vietata la vendita a privati di "armi automatiche" (cioè, che sparano "a raffica").

Ed invece, poi, ho scoperto con estrema "sorpresa" e "costernazione" che noi, in rapporto alla popolazione, siamo al secondo posto in classifica (dopo gli USA) quanto agli omicidi commessi con le armi da fuoco; precedendo, in questo triste primato, tutti gli altri Paesi europei.

E, per giunta, si tratta, nella maggior parte dei casi, di omicidi (o suicidi) perpetrati con armi da fuoco legalmente detenute!

Inoltre, almeno stando alla maggior parte dei singoli casi di cui sono venuto a conoscenza (tipo il caso Vannini), sebbene io non sia riuscito a trovare le relative statistiche, mi sembra di aver potuto rilevare che le morti per arma da fuoco che si verificano in Italia, in genere sono provocate da incidenti derivanti dall'uso improprio:

- di "pistole semiautomatiche";

- manovrate con estrema "imperizia" e "imprudenza".

***

L'unico caso al mondo di omicidio per incidente dovuto ad un "revolver", che io sappia, è quello commesso da Alec Baldwin; ma non perchè abbia manovrato il revolver con "imperizia", bensì soltanto perchè dentro c'erano pallottole vere, e non cartucce a salve come credeva lui.

In realtà;

- mentre le "pistole semiautomatiche" sono congegni alquanto complicati, che possono talvolta dar luogo ad errori fatali nel loro maneggio;

- i "revolver", invece, sono meccanismi molto più elementari, per cui è pressochè "impossibile" uccidere qualcuno "per sbaglio" (salvo il caso, più unico che raro, di Alec Baldwin).

Per cui, secondo me, salvo che le armi non siano possedute (per ragionevoli  motivi di servizio, di sicurezza o di sport) da parte di veri "esperti", i comuni cittadini, se proprio vogliono armarsi, farebbero bene ad acquistare "esclusivamente" revolver, e "mai" pistole semiautomatiche; e, questo, anche se sono dotati di regolare porto d'armi.

Basti, al riguardo, considerare che, ai fini della sicurezza:

- se impugni un revolver, lo vedi subito se è carico o meno, perchè i fondelli dei proiettili ce l'hai sotto al naso (a meno che tu non sia completamente cieco):

- se, invece, impugni una pistola semiautomatica, non vedi affatto se contiene o meno dei proiettili (sebbene un esperto abbia comunque modo di capirlo):

A parte questo, è la differente complessità di tali tipi di armi ad influire sulla minore o maggiore possibilità di incidenti!

Ed infatti, una delle lezioni base sull'uso delle armi, è lo "scaricamento" delle stesse; che, però, è molto diverso nel caso di un revolver o di una pistola.

Ed infatti:

a)

Per scaricare un revolver basta aprire il tamburo ed espellere tutti i proiettili (o i residui bossoli) che contiene, spingendoli fuori con l'apposita assicella estrattrice:

E, di sicuro, nessun idiota può non accorgersi se il tamburo è del tutto vuoto, oppure se contiene ancora qualche proiettile:

Se il tamburo è del tutto vuoto, rimettendolo al suo posto, si è sicuri che il revolver è reso del tutto inoffensivo.

b)

Per scaricare una pistola semiautomatica, invece, occorre estrarre il caricatore, e svuotarlo ad uno ad uno dei proiettili che esso contiene:

Anche in questo caso, di sicuro, nessun idiota può non accorgersi se il caricatore è del tutto vuoto, oppure se contiene ancora qualche proiettile:

Ma è qui che "casca l'asino", perchè, anche se il caricatore è del tutto vuoto, rimettendolo al suo posto, non si è affatto sicuri che la pistola sia stata resa inoffensiva; ed infatti, se prima di reinserire il caricatore vuoto, non si "scarella" la pistola, potrebbe essere rimasto un colpo in canna, il quale va assolutamente espulso.

In parole povere, in un revolver non può mai fisicamente rimanere un colpo in canna, mentre in una pistola semiautomatica sì; anzi, è abbastanza normale.
Il che è pericolosissimo!

Potrei fare altri esempi di come una pistola automatica possa provocare molti più incidenti di un revolver (come di fatto accade); ma non è  mia intenzione di fare qui un corso accelerato di maneggio delle armi.

Tutto questo "pistolotto", se mi consentite il "calembour", infatti, ha lo scopo esclusivo di indurre chi legge:

- possibilmente a non comprare affatto "pistole" (se non per specifici e ragionevoli motivi);

- se proprio le si vuole acquistare, qualora non si sia molto esperti nel loro maneggio, è preferibile comprare soltanto "revolver", e non "armi semiautomatiche" (pur possedendo la relativa licenza).

Ed infatti sono quelle che causano il maggior numero di incidenti mortali!

Ma, soprattutto, ricordatevi che esiste il numero unico europeo per le emergenze (NUE): il 112