Menu principale
Menu

Mostra messaggi

Questa sezione ti permette di visualizzare tutti i messaggi inviati da questo utente. Nota: puoi vedere solo i messaggi inviati nelle aree dove hai l'accesso.

Mostra messaggi Menu

Messaggi - Eutidemo

Pagine 1 ... 180 181 182 183 184 ... 410
#2716
Tematiche Culturali e Sociali / Re: Il paradosso delle tre carte di Weaver
16 Luglio 2022, 06:25:38 AM
Ciao Phil
Se ho ben capito, le scatole sono tre, delle quali:
A) Contiene due monete d'argento
B) Contiene due monete d'oro
C) Contiene una moneta d'oro e una d'argento.
***
Il che equivale a dire che:
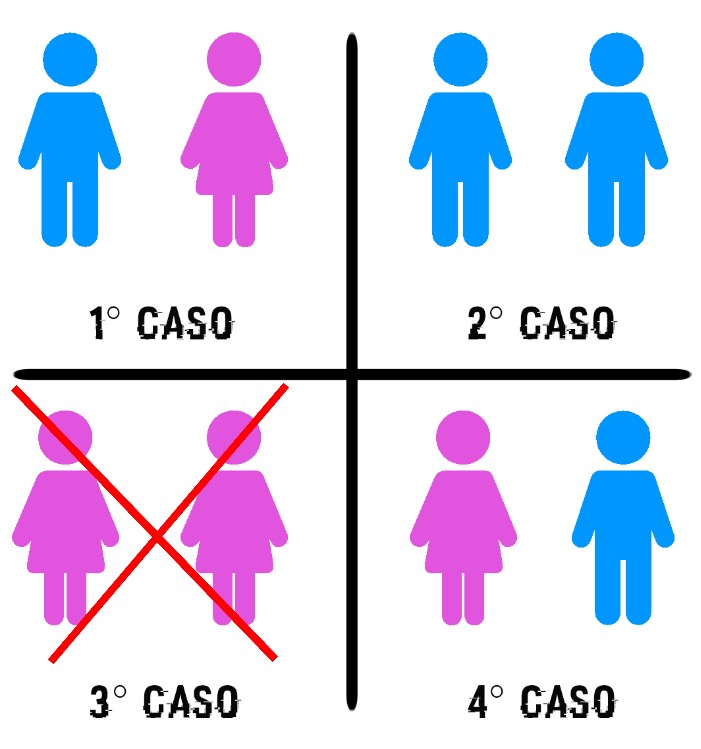
- due scatole su tre contengono due monete dello stesso metallo (A e B);
- solo una scatola su tre, invece, contiene due monete di metalli diversi (C).
***
Se le cose stanno così, è ovvio che, pescando in una scatola a caso, avrò il 66% di probabilità di beccare una scatola che contiene due monete dello stesso metallo.
Di conseguenza:
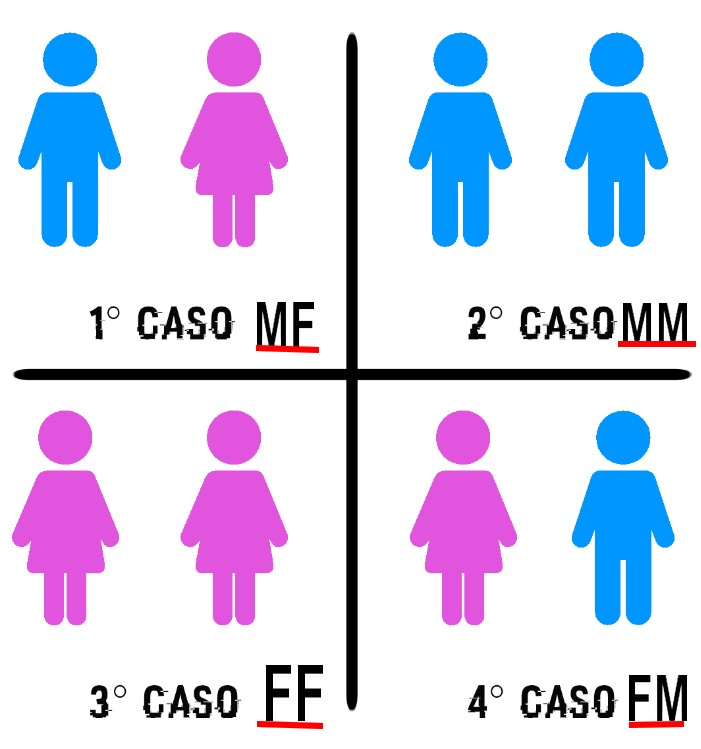
- supponendo che la prima moneta sia d'oro, le probabilità che anche la seconda moneta sia d'oro sono del 66%;
- supponendo che la prima moneta sia d'argento, le probabilità che anche la seconda moneta sia d'argento sono del 66%.
***
Ho invece solo una probabilità su tre (33%) di scegliere l'unica scatola che contiene due monete di metalli diversi (C).
Per cui:
- supponendo che la prima moneta sia d'oro, le probabilità che  la seconda moneta sia d'argento sono del 33%;
- supponendo che la prima moneta sia d'argento, le probabilità che la seconda moneta sia d'oro sono del 33%.
***
Il che, secondo me, spiega perfettamente i risultati dei tuoi test, e, in fondo, anche il paradosso delle tre carte di Weaver.
***
Ed infatti, se la carta:
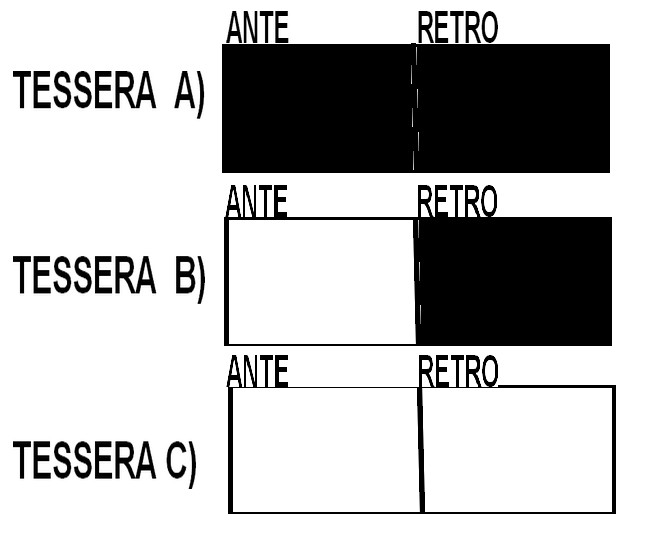
A) Contiene due lati bianchi
B) Contiene due lati neri
C) Contiene un lato bianco e un lato nero
ciò equivale a dire che:
- due carte su tre contengono due lati dello stesso colore (A e B);
- solo una carta su tre, invece, contiene due lati di colori diversi (C).
***
Se le cose stanno così, è ovvio che, anche in questa ipotesi, avrò il 66% di probabilità di estrarre a caso una carta di colore uniforme su entrambi i lati (o la carta A o la carta B).
Di conseguenza::
- supponendo che la carta che estraggo abbia un lato bianco, le probabilità che anche l'altro lato sia bianco sono del 66%;
- supponendo che la carta che estraggo abbia un lato nero, le probabilità che anche l'altro lato sia nero sono del 66%;
***
Ho invece solo una probabilità su tre (33%) di scegliere l'unica carta che contiene due lati di colori diversi (C).
***
Il che, secondo me, spiega perfettamente i risultati dei tuoi test, e, in fondo, anche il paradosso delle tre carte di Weaver; ma in modo un po' diverso da come lo spiega lui.
Ed infatti, a mio parere, messe le cose in questi termini, non c'è niente di "paradossale" nella faccenda; la quale, invece, risulta di una ovvietà banale.
***
Ma forse mi sbaglio!
***
Un saluto!
***
#2717
Tematiche Culturali e Sociali / Il paradosso dei due bambini di Gardner
15 Luglio 2022, 13:32:35 PM
Si tratta di un paradosso formulato da Martin Gardner sullo Scientific American, laddove viene così formulato: "Il signor Smith ha due bambini, almeno uno dei quali è un maschio. Qual è la probabilità che entrambi i bambini siano maschi?"
***
Spontaneamente verrebbe da rispondere che la probabilità è del 50%, mentre, invece, secondo Gardner, sarebbe solo del 33,3%.
Ed infatti, secondo lui, astrattamente i casi sarebbero i seguenti:
1° caso
Il primo bambino è un maschio e il secondo è una femmina;
2° caso
Sono due maschi;
3° caso
Sono due femmine;
4° caso
Il primo bambino è una femmina e il secondo è un maschio.
***
Ora, poichè il postulato è che il signor Smith ha due bambini, "almeno uno dei quali è un maschio", è ovvio che il terzo caso è da escludere:  ci restano, quindi, solo i casi 1, 2 e 4.
Per cui, la probabilità che i entrambi i bambini siano maschi, ovvero il caso n°2, di 1/3, ovvero del 33,3%.
***
Secondo me, invece, il caso 1 e 4 sono identici, in quanto il quesito riguarda il "sesso", e non l'"età dei figli"; per cui, a mio parere la probabilità che i entrambi i bambini siano maschi è del 50%.
***
Ed infatti, volendo, il quesito potrebbe anche essere così riformulato:
"Il signor Smith adotta due bambini, nati esattamente nello stesso istante, almeno uno dei quali è un maschio. Qual è la probabilità che entrambi i bambini siano maschi?"
In questo caso il paradosso di Gardner non reggerebbe più in alcun modo, neanche facendo ricorso al "trucco" dell'età; ed infatti, in tale caso, la probabilità che i entrambi i bambini siano maschi sarebbe senz'altro del 50%.
***
Secondo me, il "qui pro" scaturisce dall'abitudine di "codificare simbolicamente" gli elementi di un problema, anche quando non ce n'è alcuna ragione; ad esempio, distinguere MF da FM è una pura e semplice "mistificazione matematica", perchè presuppone -senza necessità- che occorra tenere conto della primogenitura dei figli, scindendo così immotivatamente in due un'ipotesi, che, invece, è unitaria.
***
Allo stesso modo, distinguere MF da FM potrebbe anche presupporre senza necessità che occorra tenere conto della altezza o del peso dei dei figli; cioè la lettera in prima posizione indicherebbe il più alto o il più pesante (invece del più vecchio).
Il che non ha senso, se il quesito riguarda solo il sesso dei figli!
***
Scrivere di avere "un figlio maschio e una figlia femmina", ovvero scrivere di avere "una figlia femmina e un figlio maschio" (a prescindere dalla primogenitura, dall'età e dal peso), logicamente significa la stessa cosa; anche se poi si scrive MF distinto da FM!
***
In effetti, almeno in parte, per certi aspetti è un po' il discorso del "fronte" e del "retro" di una carta; perchè, in realtà, delle semplici carte colorate in bianco e nero, hanno semplicemente due "lati" distinti e contrapposti, ma nessuno dei due ha il titolo per essere definito "fronte" o"retro" (come, invece, nel caso di un quadro o di un libro).
Ma questo è un altro discorso!
***
#2718
Attualità / Re: Crisi di governo
15 Luglio 2022, 11:58:30 AM
Come già saprete, il Presidente della Repubblica non ha accolto le dimissioni Di Draghi, e lo ha invitato a presentarsi al Parlamento per rendere comunicazioni; ciò, affinché si effettui, nella sede propria, una valutazione della situazione che si è determinata a seguito degli esiti della nota seduta svoltasi presso il Senato della Repubblica.
***
Di conseguenza, Draghi, durante la riunione del Cdm avrebbe detto ai ministri che mercoledì prossimo riferirà alle Camere; e così tutti i partiti avranno modo di dire la loro.
***
Qualche partito e qualche rappresentate di partito, comunque, hanno già anticipato la loro opinione; anche se non è detto che poi verrà confermata in aula.
.
1) LA LEGA
Con una nota alla stampa è stato così comunicato: "La Lega è stata leale, costruttiva e generosa per un anno e mezzo, ma da settimane il presidente Draghi e l'Italia erano vittime dei troppi No del Movimento 5 Stelle e delle forzature ideologiche del Partito democratico. La Lega, unita e compatta anche dopo le numerose riunioni di oggi, condivide la preoccupazione per le sorti del Paese: è impensabile che l'Italia debba subire settimane di paralisi in un momento drammatico come questo, nessuno deve aver paura di restituire la parola agli italiani".
.
2) INSIEME PER IL FUTURO
Luigi Di Maio ha detto: "Non è scontato l'esito di mercoledì in aula, perchè tutto dipende dalla maturità; ed infatti serve un atto di maturità e non solo di responsabilità da parte delle forze politiche. Spero che domani lo si possa già fare e che ci sia la volontà di farlo!"
.
3) FRATELLI D'ITALIA
Giorgia Meloni ha detto: "Non accettiamo scherzi, per FdI questa legislatura è finita e daremo battaglia perché si restituisca ai cittadini quello che tutte le democrazie hanno e cioè la libertà di scegliere da chi farsi rappresentare per fare cosa".
.
4) PARTITO DEMOCRATICO
Con una nota alla stampa è stato così comunicato: "Ora solo al lavoro perché mercoledì alle Camere si ricrei la maggioranza e il Governo Draghi possa ripartire. Il Paese piomba in una crisi gravissima che non può permettersi".
 .
5) ITALIA VIVA
Renzi ha detto: "Giuseppe Conte è come quei clown che non fanno più ridere, alla fine della carriera. Sta imponendo il suo narcisismo e la sua presenza in tutti i canali senza offrire una sola soluzione ai problemi del Paese".
.
6) FORZA ITALIA
Antonio Tajani ha detto:"Complimenti al M5S per aver fatto questo guaio mentre c'è una crisi in corso, c'è una guerra ai confini dell'Europa, già la Borsa oggi è crollata, lo Spread sale, c'è un'impennata dei prezzi di tutte le materie prime. E' da irresponsabili aver provocato questo caso, con un'arroganza e con dei ricatti che sono inaccettabili".
.
7) MOVIMENTO 5 STELLE
Giuseppe Conte ha detto: "Il M5s ha dato sostegno a questo governo sin dall'inizio con una votazione sui pilastri della della transizione ecologica e della giustizia sociale. Non chiediamo posti, nomine, nulla, ma chiediamo ovviamente di rispettare un programma definito all'inizio: transizione ecologica e urgenza della questione sociale che adesso è esplosa. O ci sono risposte vere, strutturali e importanti opporre nessuno può avere i nostri voti".
***
il sindaco di Roma Roberto Gualtieri, "a latere", ha detto: "Se mi sento in colpa e se è colpa di Roma e del termovalorizzatore questa crisi di governo? No, non è colpa di Roma. Noi facciamo le scelte giuste!".
***
Giudicate voi! :)
***
#2719
Tematiche Culturali e Sociali / Re: Il paradosso delle tre carte di Weaver
15 Luglio 2022, 06:01:18 AM
Ciao Phil. :)
Innanzittutto di ringrazio per aver effettuato  il test, con tre serie simulate da 1000 estrazioni ciascuna; numero che mi sembra abbastanza consistente per poter risultare significativo.
Da tale triplice test, se in verticale appare la percentuale di volte in cui il fronte e il retro sono del medesimo colore (o solo BB o solo NN), e in orizzontale appare il numero di estrazioni, mi sembra di capire che, "di fatto", la percentuale di volte in cui il fronte e il retro sono del medesimo colore supera "sempre" il 60%; il che, secondo me, dovrebbe essere già di per sè sufficiente a dimostrare "materialmente" la tesi di Weaver.
***
Presumo, però, che quando tu scrivi che il test indica quante volte escono carte nelle quali il fronte e il retro sono del medesimo colore, tu ti riferisca:
- o solo al caso della carta BB
- o solo al caso della carta NN
Ed infatti solo in tale ipotesi sarebbe "materialmente" dimostrata la tesi di Weaver.
***
Se, invece, il test indica quante volte escono carte nelle quali il fronte e il retro sono del medesimo colore, ma indifferentemente BB o NN, mi sembra che il risultato dei grafici indichi una cosa completamente diversa.
***
Ed infatti, se le carte in gioco sono tre:
A) BB
B) NN
C) Doppio colore (cioè, da un lato bianca e dall'altro nera BN o NB)
E' ovvio che, estrandole a sorte:
a)
A) BB e B) NN uscirano complessivamente con una percentuale media del 66%; cioè, in media, due volte su tre.
b)
La carta C) (cioè, da un lato bianca e dall'altro nera BN o NB), uscirà, invece, solo il 33% delle volte; cioè, in media, una volta su tre.
***
Il che è "ovvio", perchè le carte sono in tutto tre.
***
Per cui, secondo me, in tal caso, il test non dimostrerebbe in alcun modo la tesi di Weaver!
***
Ti prego, quindi, di chiarire tale punto, grazie!
***
Un saluto! :)
***
#2720
Attualità / Re: Oggi 14 Luglio! Ma la musica della Marsigliese l'ha composta un italiano!
15 Luglio 2022, 05:21:17 AM
Citazione di: anthonyi il 14 Luglio 2022, 07:40:48 AMLa cosa non mi meraviglia, eutidemo, d'altronde noi siamo la patria della musica.
Certo quei nazionalisti di francesi qualche merito potrebbero pure riconoscercelo pubblicamente, già si inventarono qualche anno fa che il nostro genio Leonardo da Vinci era cosa loro. D'altronde bisogna capirli, già un po' rosicano del fatto che il dipinto più famoso, del loro museo nazionale, sia stato fatto da un italiano, pensa se uno gli insinua che il loro inno nazionale é un plagio della creatività italiana. Io ci andrei cauto, la Francia é sempre una potenza nucleare! 😬
Senza contare che pure Napoleone B(u)onaparte era italiano; corso ma di nobili ascendenze toscane ;)
#2721
Attualità / Oggi 14 Luglio! Ma la musica della Marsigliese l'ha composta un italiano!
14 Luglio 2022, 06:15:48 AM
In seguito all'invasione da parte dell'Austria, il sindaco di Strasburgo, ordinò al compositore e poeta Rouget de Lisle, all'epoca ufficiale del genio militare, di scrivere un canto di guerra, per incitare i cittadini francesi ad arruolarsi come volontari per combattere l'invasore austriaco; il compositore raccontò che la sera del 26 aprile 1792, nel tornare a casa in rue de la Mésange, "ebbe l'ispirazione" e compose  l'inno "Chant de guerre pour l'Armée du Rhin" ("Canto di guerra per l'Armata del Reno").
***
Solo successivamente assunse il nome di "Marseillaise" ("Marsigliese") perché cantata per le strade parigine dai volontari ("fédérés") provenienti da Marsiglia al loro arrivo a Parigi; e così divenne la chiamata generale alle armi della Rivoluzione Francese.
***
Però, l'anno prima, nel 1791, il  compositore italiano Giovanni Battista Viotti, aveva creato una composizione sinfonica denominata "Tema e Variazioni in Do maggiore"; la quale, musicalmente,  risulta molto simile (a dir poco) alla "Marsigliese"; soprattutto nei passi "topici", dove, secondo me, è praticamente identica!
Ascoltate e giudicate voi!
https://www.youtube.com/watch?v=gmXtg3WnQTY
***
#2722
Tematiche Culturali e Sociali / Re: Il paradosso delle tre carte di Weaver
14 Luglio 2022, 05:53:24 AM
Ciao Phil. :)
Hai ragione, se guardiamo l'esperimento dal "lato" nero, la combinazione "NB" è uscita 2 volte, quella "NN" 5 volte, ossia 5 volte su 7 la tessera nera aveva anche l'altro lato nero; cioè si tratta del 71% dei casi, addirittura superiore al 66% previsto.
***
Però non sono affatto d'accordo che  un campione così piccolo (il nero) rappresenti meglio la probabilità standard di una casistica più estesa (quella del bianco, 26 su 33); ed infatti, secondo me, meno una casistica è estesa e meno significative sono le interpretazioni statistiche che se ne possono trarre, mentre più una casistica è estesa e più significative sono le interpretazioni statistiche che se ne possono trarre.
***
Ad esempio:
- se tiriamo in aria la moneta 7 volte, e 5 volte su 7 esce testa, non c'è niente di particolarmente strano;
- ma se, invece, tiriamo in aria la moneta settemila volte, e cinquemila volte su settemila esce testa, la faccenda diventa alquanto sospetta.
***
D'altronde, anche tu hai giustamente scritto che: "...la probabilità non è la realtà, ma una sua stima sempre più attendibile quanto più il numero di casi tende asintoticamente all'infinito."
***
Ti ringrazio per il LINK, ma a causa della mia scarsa competenza "cibernetica", mi riesce alquanto difficoltoso usarlo; non vorrei trarne risultati aberranti.
Perchè non fai tu stesso due o tre volte il test (almeno per qualche centinaio se non per qualche migliaio di "estrazioni" veloci e automatiche), e poi ci "trasli" e "traduci" nel modo più comprensibile e corretto possibile il risultato al caso delle tessere, per riscontrare se effettivamente, apparendo un lato visibile bianco,  in 2 casi su 3 anche il lato non visibile è bianco?
Cioè, per verificare che  il lato non visibile sia effettivamente bianco è (più o meno) del 66,6%, su un numero davvero consistente di "estrazioni"?
Mi fido ciecamente della tua onestà e della tua competenza!
***
Un saluto! :)
***
#2723
Tematiche Culturali e Sociali / Il paradosso delle tre carte di Weaver
13 Luglio 2022, 11:44:59 AM
Il paradosso delle tre carte di Weaver può essere formulato in varie modi; ma, sostanzialmente, se l'ho ben compreso, consiste in questo:
- abbiamo un bussolotto, o una scatola, con dentro tre carte o tre tessere;
- una carta, o una tessera, ha entrambi i lati bianchi, una entrambi neri e una uno bianco e uno nero;
- se estraiamo una carta, o una tessera, e, guardando un solo lato, esso è bianco, che probabilità c'è che anche l'altro lato sia bianco?
***
Secondo Weaver, ed anche in base al "Teorema di Bayes",  sapendo che il lato visibile è bianco, ci troviamo in uno dei seguenti tre casi:
1: Lato visibile Bianco (fronte) e lato non visibile Bianco (retro);
2: Lato visibile Bianco (retro) e lato non visibile Bianco (fronte);
3: Lato visibile Bianco, lato non visibile Nero.
Pertanto, visto che in 2 casi su 3 il lato non visibile è bianco, la probabilità che esso sia effettivamente bianco è del 66,6%.
***
Tale ragionamento, formalmente, mi sembra assolutamente corretto; però vorrei valutarlo anche secondo il "Metodo di analisi delle ipotesi confliggenti", da me illustrato in un mio apposito TOPIC.
https://www.riflessioni.it/logos/tematiche-culturali-e-sociali/metodo-di-analisi-delle-ipotesi-confliggenti/
.
SPERIMENTALMENTE
A tal fine, consideriamo:
LA TESSERA A), che è nera da entrambi i lati;
LA TESSERA B), che è bianca davanti e nera di dietro;
LA TESSERA C), che è bianca da entrambi i lati.
***
E poi mettiamole in una scatola.
***
Fatto ciò agitiamo la scatola, come se fosse un bussolotto, ed estraiamo di volta in volta una tessera.
(password: "logos")
https://www.dailymotion.com/video/x8cfqva
***
Il risultato è stato che, nelle 26 volte in cui ci è apparso un "lato visibile bianco":
- per 14 volte l'altro lato era nero;
- per 12 volte l'altro lato era bianco.
***
Quindi, in questo caso, ed in altri che ho sperimentato con degli amici sostenitori della teoria di Weaver, la sua teoria non sembra affatto funzionare.
***
Provateci anche voi! ;)
***
Ovviamente, per avere dei risultati davvero "probanti":
- bisognerebbe utilizzare tessere e bussolotti molto più "professionali" e "randomici" di quelli che ho usato io;
- inoltre bisognerebbe effettuare il test almeno qualche centinaio (se non qualche migliaio) di volte.
***
Per cui sono io il primo ad ammettere che il mio "videoclip" non dimostra assolutamente niente; sebbene sia quantomeno singolare che altri due o tre esperimenti fatti con degli amici, abbiano dato risultati sempre intorno al 50% (a volte un po' di più, a volte un po' di meno, ma mai con uno scarto significativo).
E la cosa singolare è che le stesse medie, più o meno, si ottengono sia ad occhi chiusi che ad occhi aperti!
Provate anche voi, se vi volete togliere lo sfizio.
.
TEORICAMENTE
Sotto il profilo teorico, secondo me, il ragionamento matematico di Weaver funziona perfettamente "contando" astrattamente il numero delle "facce"; però non funziona per niente se teniamo conto  concretamente solo del numero delle "tessere".
Ed infatti:
.
1)
Se ci esce una tessere con una  "faccia" bianca, in realtà, le possibili tessere in ballo restano soltanto due (B e C); ed infatti, la tessera con due facce nere (A) esce dal gioco, e serve solo a confonderci le idee.
L'inverso, ovviamente, avviene se ci esce una tessere con una  "faccia" nera!
.
2)
Di conseguenza, se le possibili tessere in ballo restano soltanto due (B e C o A e B), la probabilità che esca l'una o l'altra non può che essere mediamente del 50%, a nulla rilevando il colore delle loro facce, che noi lo si conosca o meno.
.
Però, come ho detto, quella da me prospettata, è solo un'"ipotesi confliggente"; ed infatti anche il ragionamento di Weaver, a mio parere, configura un'ipotesi matematicamente plausibile.
.
P.S.
L'ideale, sarebbe un programma di computer che effettui automaticamente il test per migliaia di volte, e poi verifichi di fatto se è vero che, apparendo un lato visibile bianco,  in 2 casi su 3 anche il lato non visibile è bianco; cioè che  la probabilità statistica che esso sia effettivamente bianco è del 66,6%.
L'ho anche cercato, un programma del genere, ma non l'ho trovato!
Se lo trovate fatemelo sapere e facciamo una prova più seria di quella "casareccia" che ho fatto io ;)
***
#2724
Tematiche Culturali e Sociali / Re: Il paradosso del "sorite", il paradosso della "colonia" e quello dello "zigote"
12 Luglio 2022, 11:47:33 AM
Ciao Anthony. :)
Hai ragione nel dire che non esiste un momento "giusto" per praticare qualcosa di "non giusto"; però può esistere un momento "non giusto" per praticare qualcosa di "giusto".
Il mio topic si occupava di questo secondo aspetto, non del primo!
***
Quanto al criterio per distinguere un essere umano "in potenza" o "in atto", tu, secondo me, fai soltanto dei discorsi di caratterere prettamente paralogistico; ed infatti non posso credere che tu possa equiparare eticamente la soppressione di uno "zigote" alla soppressione di un "bambino" che sta per nascere.
Ed infatti si tratta di due entità "ontologicamente" differenti; a nulla rilevando che la prima, sviluppandosi, potrebbe diventare la seconda.
***
Si diceva che ogni soldato di Napoleone  avesse nello zaino il "bastone di maresciallo"; ma, finchè non diventata un maresciallo, restava comunque un soldato semplice!
Per cui, se veniva ucciso, moriva un soldato semplice, e non un maresciallo dell'Impero!
***
Non è mai stata mia intenzione distinguere tra "vita" e "non vita" umana, bensì  tra "vita non ancora umana", e "vita ormai divenuta umana"; si tratta di una distinzione ben diversa.
***
Quanto al requisito della "sofferenza" o del "peso", si tratta di argomenti "ultronei" del tutto estranei al tema; fatti solo per confondere le acque!
***
Sono invece perfettamente d'accordo con te che l'aborto, in sè e per sè (anche se eseguito nella prima settimana), non può in nessun caso essere considerato un "bene"; ed infatti, per la donna, è comunque un evento traumatico, che sarebbe molto meglio evitarle per il tramite di un'oculata strategia contraccettiva.
***
Un saluto :)
***
#2725
Tematiche Culturali e Sociali / Re: Il paradosso del "sorite", il paradosso della "colonia" e quello dello "zigote"
12 Luglio 2022, 07:05:04 AM
Ciao Anthony. :)
Non mi sembra affatto che tu sia "pedante", perchè, se tu sei "antiabortista", è ovvio che il mio topic non ti si confaceva minimamente.
***
Ed infatti, l'oggetto del mio topic:
- non riguardava minimamente la liceità etica dell'aborto in quanto tale;
- riguardava, invece, una volta ritenutolo eticamente lecito, quale fosse il momento più "giusto" per praticarlo.
***
Il che non significa affatto minimizzare o falsificare la drammaticità dell'aborto, ma, al contrario, significa conferire a tale atto una estrema importanza e rilevanza; perchè, almeno dal mio punto di vista, un conto è eliminare due o tre cellule che si sono appena aggregate, ed un altro conto è sopprimere un bambino nel ventre della madre, poco prima della nascita (atto, questo, che trovo del tutto "ripugnante", e sostanzialmente equiparabile all'"omicidio" -vedi Pretura Arezzo, 11 luglio 1992, Giust. pen. 1992, II, 601-).
***
Secondo me è assurdo "omologare" le due cose!
***
Tanto è vero che quasi tutte le legislazioni del mondo distinguono giuridicamente le due condotte; per non essendo d'accordo sul "punctum distinctionis".
***
Quando io dico che c'è un momento nel quale l'aggregazione cellulare conseguente alla copula "non è ancora effettivamente umana", non solo non "filosofeggio", ma, anzi, dico una cosa assolutamente "ovvia"; della quale non ci sarebbe neanche necessità di discutere seriamente.
Sarebbe come discutere della differenza che c'è  tra una ghianda e una quercia; ed infatti mi pare ovvio che una "ghianda" non ha niente a che vedere con una "quercia" (anche se, in origine, "in potenza" lo era stata).
***
Quando tu scrivi che: "l'umanità é un processo, e ha i suoi stadi, se ne blocchi uno, elimini tutte le potenzialità future" dici una cosa che è vera, ma solo in parte; ed infatti, esistono senz'altro  sia la "quercia" che l'"uomo", ma la "quercità" e l'"umanità" di un determinato processo, sono solo della "astrazioni" metafisiche!
Ed infatti, se ci pensi bene:
- dire che "l'umanità é un processo, e ha i suoi stadi, per cui se ne blocchi uno, elimini tutte le potenzialità future";
- è come dire "la  é quercità è un processo, ed ha i suoi stadi, per cui se ne blocchi uno, elimini tutte le potenzialità future".
***
Ma l'etica, così come il diritto, almeno sotto certi aspetti, riguardano soltanto quello che è "attuale", e non quello che è "in potenza"!
Ed infatti, ai sensi dell'art.635 c.p., chi abbatte una quercia senza la debita autorizzazione è sanzionato penalmente; ma dare le ghiande in pasto ai maiali, anche se "in potenza" esse sarebbero potute diventare delle quercie, non costuisce alcun tipo di reato.
***
Beninteso, questo senza voler minimamente equiparare qualitativamente una "ghianda" (che non è nemmeno "animale", ma solo "vegetale") ad uno "zigote"!
Ci mancherebbe altro!
***
Dal punto di vista filosofico, si può benissimo avere una concezione diversa dell'etica; e considerare contraria a quest'ultima non solo qualsiasi "interruzione della gravidanza" (anche il giorno successivo al concepimento), ma anche qualsiasi "impedimento della gravidanza" grazie all'uso di contraccettivi.
Anche in questo modo, infatti, sia pure ancora più "anticipatamente", si impedisce che possa nascere un bambino.
***
Però ripeto che l'oggetto del mio topic:
- non riguardava minimamente la liceità etica dell'aborto in quanto tale;
- riguardava, invece, una volta ritenutolo eticamente lecito, quale fosse il momento più "giusto" per praticarlo.
***
Non vedo come questo, secondo te, dovrebbe portare a "minimizzare e a falsificare la drammaticità dell'aborto, a cercare in ogni modo di evitare che le potenziali madri prendano coscienza di questa drammaticità."
Non ho mai scritto niente in tal senso; anzi, esattamente il contrario!
***
Un saluto! :)
***
#2726
Tematiche Culturali e Sociali / Re: Il paradosso del "sorite", il paradosso della "colonia" e quello dello "zigote"
11 Luglio 2022, 13:11:55 PM
Ciao Iano. :)
Io e te potremmo anche decidere di definire "mucchio" un insieme che contenga più di 5 elementi; ma altri partecipanti al FORUM, potrebbero, altrettanto legittimamente, decidere di definire mucchio un insieme che contenga più di 6 o 7 o 8 elementi.
Secondo la TRECCANI, il "mucchio" è definito come: "Una quantità di materiale o di oggetti ammassati disordinatamente uno sull'altro in forma all'incirca conica; ovvero, in senso estensivo e/o figurativo, una notevole  quantità di cose concrete o astratte."
Quindi, per definizione, un "mucchio" non corrisponde mai, per tutti, ad uno specifico "numero" di elementi!
***
Come tu giustamente scrivi, quindi,  non esiste una scelta "oggettiva", scontata per tutti, del "giorno preciso" o dell'"ora precisa" in cui il raggruppamento di cellule staminali dà luogo ad un "bambino" (sebbene in senso lato ed ancora e nel grembo materno) ; il che, quindi, comporta una  inevitabile disuniformita' legislativa da Paese a Paese.
***
D'altronde, anche in altri campi, ogni Paese si regola a modo suo.
Ad esempio:
- in Italia l'evasione fiscale cessa di essere un semplice "illecito amministrativo", e diventa un "reato penale" quando l'imposta supera i 30 mila Euro;
- in Germania, invece, l'evasione fiscale cessa di essere un semplice "illecito amministrativo", e diventa un "reato penale" quando l'imposta supera i 20 mila Euro (mi sembra).
***
Anche in questo caso, torniamo al "paradosso del sorite", perchè non esiste un criterio logico universale per stabilire quale sia la "soglia di evasione" che configuri "reato" in qualsiasi parte del mondo!
***
Per cui, come giustamente scrivi tu: "Non essendoci una "scelta che si proponga da se" siamo costretti ad usare il nostro libero arbitrio con tutte le problematiche etiche connesse, se non trattiamo di sassi."
***
Un saluto! :)
***
P.S.
Ovviamente, come ho già argomentato nel mio topic iniziale, il raggruppamento di cellule che poi daranno luogo ad un essere umano, non può in alcun modo essere "qualitativamente" paragonato ad un raggruppamento di sassi; ed infatti, a parte il fatto che questi ultimi sono inanimati, per quanti se ne possano "ammucchiare", essi non daranno mai luogo a qualcosa di "qualitativamente" diverso dai singoli sassi.
#2727
Tematiche Culturali e Sociali / Re: Il paradosso del "sorite", il paradosso della "colonia" e quello dello "zigote"
11 Luglio 2022, 12:41:56 PM
Ciao Anthony :)
Non c'è dubbio alcuno che la vocazione del "ginecologo" (rectius dell'"ostetrico") é quella di far nascere vivi "i bambini"; ma, come da me argomentato, uno "zigote" -o anche una "morula"- non è ancora un "bambino".
***
In effetti, salvo a voler "filosofeggiare" aristotelicamente sui concetti di "potenza" e di "atto", uno "zigote" o anche una "morula" non hanno ancora niente a che vedere con un "bambino"; così come una "ghianda" non ha niente a che vedere con una "quercia" (anche se, in origine, "in potenza", lo era stata).
***
Il lavoro dei ginecologi, come anche per le altre specializzazioni mediche, é quello di salvare le "vite umane"; ma non di salvare qualsiasi cosa possa costituire "materia vivente" (cioè, la "vita" in generale), anche se non "umana" o "non ancora  effettivamente umana".
***
Un saluto! :)
***
#2728
Tematiche Filosofiche / Re: Credete nel libero arbitrio?
11 Luglio 2022, 10:54:39 AM
Quando, nel 1512, Michelangelo completò l'affresco sul soffitto della Cappella Sistina, considerata una delle opere più famose della storia dell'arte, i cardinali responsabili della cura delle opere rimasero per ore a guardare e ammirare il magnifico affresco.
***
Però, dopo l'analisi si riunirono con Michelangelo, e gli chiesero di rettificare un piccolo dettaglio apparentemente senza importanza.
Michelangelo, infatti, aveva disegnato il pannello della creazione dell'uomo con le dita di Dio e di Adamo, entrambe tese, che si toccavano; i cardinali, invece, chiesero che non si toccassero, ma che le dita di entrambi fossero separate.
Anzi, che il dito di Dio fosse sempre teso al massimo, ma che quello di Adamo si contraesse nell'ultima falange!
Un dettaglio semplice, ma con un significato ben preciso: Dio è lì, col dito teso, ma la decisione di cercarlo dipende dall'uomo:
- se vuole stenderà il dito e lo toccherà;
- ma se non vuole può passare tutta la vita senza cercarlo.
L'ultima falange del dito contratto di Adamo rappresenta così il LIBERO ARBITRIO!
#2729
Tematiche Culturali e Sociali / Re: Il paradosso del "sorite", il paradosso della "colonia" e quello dello "zigote"
11 Luglio 2022, 10:36:35 AM
@Ipazia
Sono perfettamente d'accordo con te che  anticipare i tempi dell'ivg è il modo migliore per limitare i danni sia all'adulta che al concepito; per cui trovo "gravissimo" che alcune istituzioni mediche, col loro boicottaggio burocratico, allunghino senza motivo i tempi dell'intervento.
Il che, a volte, avviene addirittura contrastando il tempestivo intervento farmacologico nelle primissime fasi in cui la definizione "grumo di cellule" è incontrovertibilmente tale; come nel "paradosso del sorite" con solo due o tre sassi.
***
D'altronde, se un medico non se la sente in coscienza di praticare aborti secondo le modalità di legge (benchè sia consentito anche dal suo "giuramento professionale"), non vedo perchè mai, tra le tante specializzazioni mediche, debba scegliere proprio "ginecologia"; ed infatti, se sceglie di specializzarsi in "odontoiatria", guadagnerà molto di più, e non correrrà il rischio che qualche sua cliente gli chieda di abortire.
Salvo il caso di qualche cliente molto sprovveduta! ;D
#2730
Scienza e Tecnologia / Re: Il "Cornershot" potrebbe ridurre le vittime dei combattimenti urbani
11 Luglio 2022, 09:20:50 AM
Citazione di: anthonyi il 10 Luglio 2022, 13:57:11 PMHo l'impressione, però, che un meccanismo del genere rende l'arma molto imprecisa per via del rinculo anomalo. A questo punto molto meglio un'arma ancorata a un punto rigido, e magari teleguidata.
Non saprei, perchè non ho mai provato quell'aggeggio!
Però io mi preoccuperei molto di più delle anomalie del "rilevamento" (sollevamento della canna), che non del "rinculo"; ed infatti  è il primo che influisce di più sulla precisone del tiro!
Pagine 1 ... 180 181 182 183 184 ... 410