Ciao Iano  .
.
 .
.Circa le tue interessantissime (e per niente "peregrine") considerazioni, osservo quanto segue:
.
1)
Quando mi ''definisco'' un avvocato ''fra virgolette'', non sto affatto usando il termine "definizione" in modo volutamente ambiguo, ma, al contrario, ne sto semplicemente evidenziando la specifica "valenza tecnica" nel contesto della mia argomentazione; ed infatti, se è vero che, talvolta, si mette ''fra virgolette'' una parola per far capire che la si sta usando in modo ambiguo, è anche vero che, invece, altre volte si mette ''fra virgolette'' una parola solo per evidenziarne la specifica "valenza tecnica" nel discorso.
***
Ed infatti, si può parlare di un avvocato:
- sia in "senso tecnico" di professionista iscritto all'Albo;
- sia in "senso generico" (come, ad esempio, "non farmi sempre l'avvocato del diavolo", oppure "sei il solito avvocato delle cause perse" ecc. ecc.).
***
Per cui, tutto il tuo discorso sul passato e sul presente della pratica forense, mi sembra un po' un "arrampicarsi sugli specchi"; anche considerando che, ad esempio, nell'antica Roma gli "avvocati", così come concepiti oggi, non esistevano!
Ed infatti, al suo posto, in genere esistevano due figure ben distinte tra di loro:
- il "giurisperito", che studiava la causa al tavolino;
- l'"oratore", che andava a dibatterla in aula.
***
Semmai il mio difetto è di usare troppe "virgolette", anche a sproposito; un vizio di cui mi vergogno e di cui mi scuso! 

***
.
2)
Quanto al mio quesito iniziale, non saprei immaginare NIENTE:
- di più chiaro;
- di meno ambiguo.
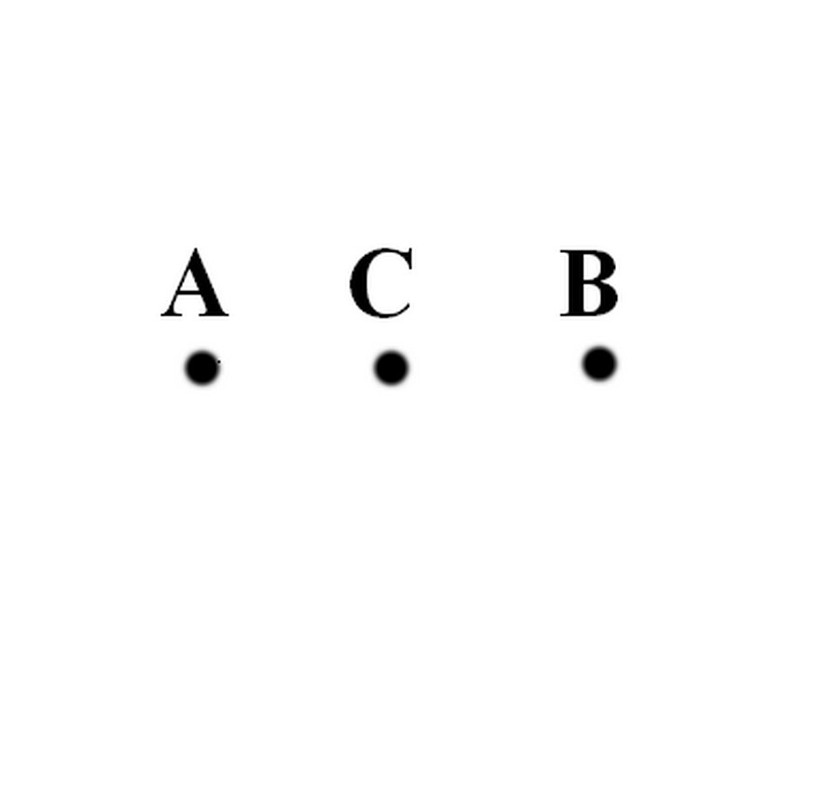
Ed infatti io avevo semplicemente chiesto: "Qual'è l'entità geometrica che costituisce la distanza minima tra il punto A ed il punto B?"
Più chiaro di così si muore!
***
Ora, tu hai risposto che l'entità geometrica che costituisce la distanza minima tra il punto A ed il punto B, nello spazio euclideo si chiama "segmento di retta"; risposta, che, in effetti, non era affatto del tutto "sbagliata", però era decisamente "incompleta".
***
Ed infatti, se tu mi avessi risposto che l'entità geometrica che costituisce la distanza minima tra il punto A ed il punto B, nello spazio euclideo era un "segmento infinitesimale di retta", io te l'avrei passata sicuramente per "buona".
***
Ed infatti la "DISTANZA MINIMA" tra il punto A ed il punto B, non è un qualsiasi "segmento di retta" (che può essere lungo un metro, un centimetro un millimetro ecc.), bensì soltanto il "segmento di retta più corto possibile"; e, cioè, almeno secondo la tua concezione geometrica, un "segmento infinitesimale di retta".
***
Io avrei senz'altro accettato una simile risposta, in quanto per me (ma non certo per i "matematici ufficiali", almeno da colonnello in su), un "segmento infinitesimale di retta" non è altro che un "punto".
Ed infatti, poichè un "segmento di retta" è costituito da "infiniti punti", se dividiamo tale segmento all'infinito, otterremo inevitabilmente un "1 punto"; ovvero anche, se tu preferisci la definizione, un "segmento infinitesimale di retta".
***
La risposta al mio chiarissimo quesito, per me sarebbe andata bene in entrambi i casi.
***
.
3)
Ed invero, la diatriba circa il fatto che:
- un "punto" non ha dimensioni;
- mentre "segmento infinitesimale di retta", invece, ha dimensioni;
costituiva una questione diversa, da quella posta con la mia domanda, la quale richiederebbe un TOPIC a parte.
***
Qui dirò solo, molto sinteticamente (e con orrore dei matematici), che, almeno per me il "punto" è quel "segmento infinitesimale di retta" del quale non se ne può concepire uno più corto.
Il che, però, con buona pace di Euclide, secondo me non vuole affatto dire che il "punto" sia "privo di dimensioni", poichè ciò che è privo di dimensioni non può esistere neanche nel mondo astratto della geometria.
Ed infatti se noi sommiamo una entità geometrica priva di dimensioni ad un'altra entità geometrica priva di dimensioni, secondo la (mia) logica, otterremo una terza entità geometrica priva di dimensioni; 0 + 0 = 0.
E così sarebbe se sommassimo all'infinito entità geometriche prive di dimensioni; così come se sommassimo all'infinito degli zeri.
Ma poichè, invece, sommando un numero infinito di "punti" otteniamo un "segmento di retta", il quale costituisce sicuramente una "figura geometrica" dotata della dimensione della "lunghezza", ne deduco, "a contrario", che anche gli elementi che compongono tale "segmento di retta" debbono necessariamente avere anche una loro una sia pur "infinitesimale dimensione".
Ed invero, almeno secondo me, avere una dimensione "incommensurabile", non vuol dire non avere alcuna "dimensione".
***
Un cordiale saluto! 

***