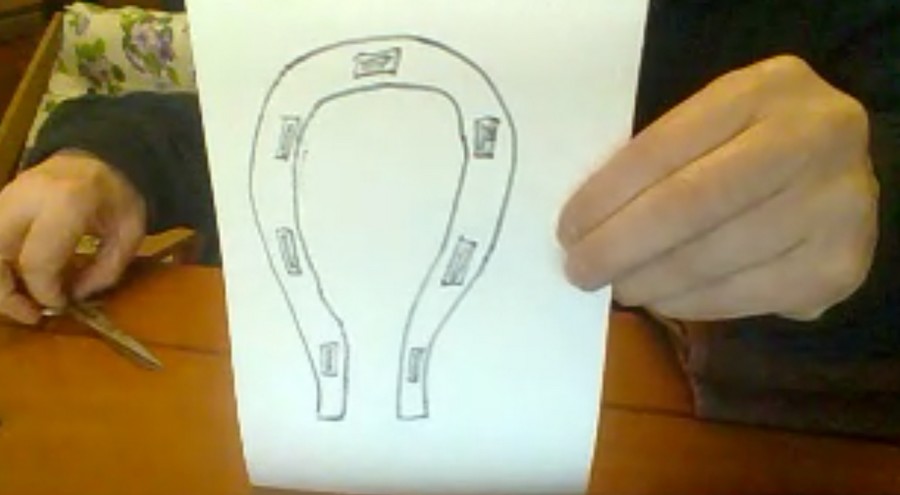
Disegnate, su un foglio di carta, un ferro di cavallo, con i suoi sette fori rettangolari da utilizzare per inchiodarlo allo zoccolo; più o meno, così come io, molto approssimativamente, ho disegnato quello qui sotto.
***
Ora, con "due soli tagli", effettuati in "linea retta" (il meglio possibile), con un paio di forbici da cucito, dovete fare in modo che, sul ferro di cavallo da me disegnato (e da voi riprodotto il meglio possibile), ognuno dei sette fori risulti separato da tutti gli altri (o da uno o più tagli di forbici e/o da uno o più tratti di pennarello); il foglio non può essere piegato o arrotolato in nessun modo, ma deve subire i due tagli senza alcun tipo di preventiva piegatura e/o arrotolatura.
Buon divertimento!
P.S.
Possibilmente, dovreste esporre la vostra soluzione in "video"; o, quantomeno, in "foto" con adeguate spiegazioni.
Buon divertimento!

P.S.
Possibilmente, dovreste esporre la vostra soluzione in "video"; o, quantomeno, in "foto" con adeguate spiegazioni.