Ciao Bobmax. 
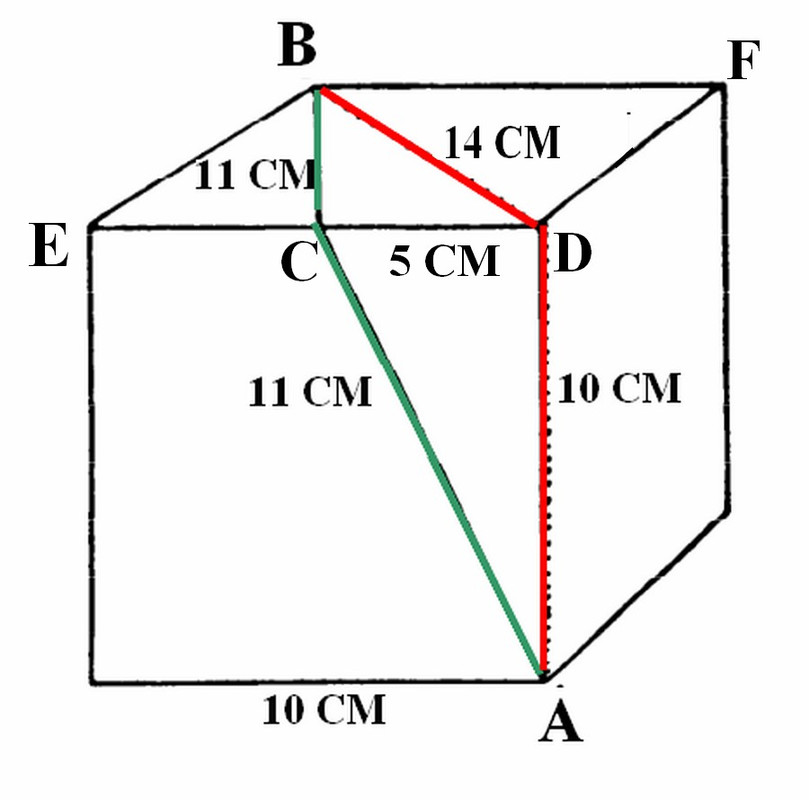
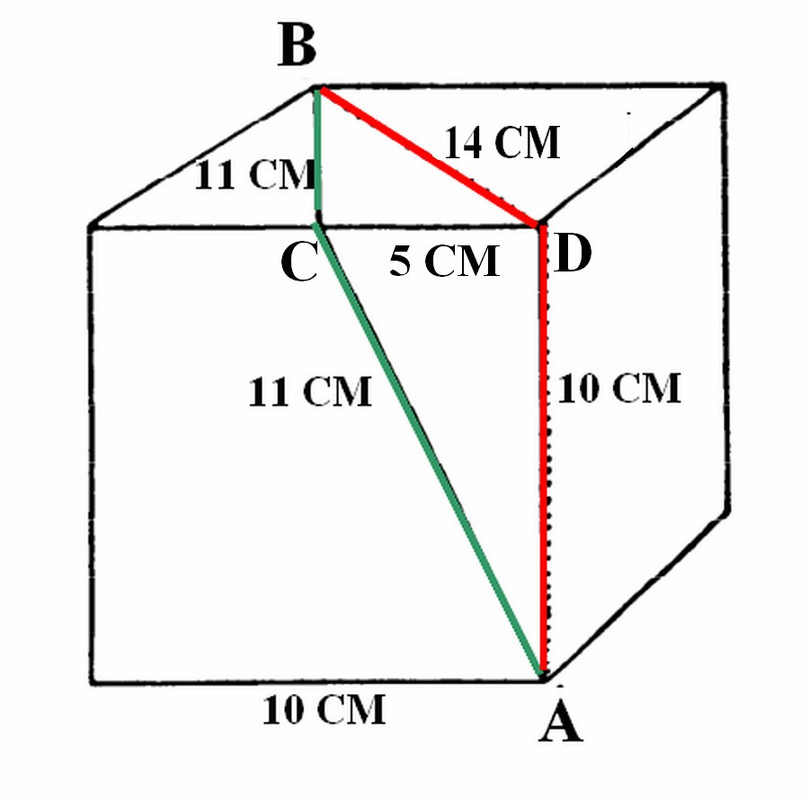
La tua aggiunta è "correttissima", però mi sembra inutilmente complicata; ed infatti, se il segmento CD è lungo 5 cm, in quanto pari ad una metà del lato, allora è ovvio che anche il segmento EC, cioè l'altra metà del lato, deve essere per forza lungo 5 cm.
Un cordiale saluto!

La tua aggiunta è "correttissima", però mi sembra inutilmente complicata; ed infatti, se il segmento CD è lungo 5 cm, in quanto pari ad una metà del lato, allora è ovvio che anche il segmento EC, cioè l'altra metà del lato, deve essere per forza lungo 5 cm.
Un cordiale saluto!


 , se un lato è lungo 10 cm, ne consegue, logicamente, che mezzo lato è per forza lungo <<5 cm>>.
, se un lato è lungo 10 cm, ne consegue, logicamente, che mezzo lato è per forza lungo <<5 cm>>.