Citazione di: Pensarbene il 13 Febbraio 2024, 13:36:52 PMe quindi?...e quindi, per citare Forrest Gump (Tom Hanks): "Stupido è chi cose stupide fa!"
- Benvenuto su LOGOS.
LOGOS - Il forum di RIFLESSIONI.IT
Questa sezione ti permette di visualizzare tutti i messaggi inviati da questo utente. Nota: puoi vedere solo i messaggi inviati nelle aree dove hai l'accesso.
#841
Storia / Re: Sintesi estrema della storia dell'architettura (e dell'uomo)
13 Febbraio 2024, 15:46:43 PM #842
Varie / Re: L'enigma dell'eredità
13 Febbraio 2024, 15:37:29 PMCitazione di: bobmax il 13 Febbraio 2024, 12:11:53 PMMa no Eutidemo, vi riesci senz'altro.Ma non sono, più o meno, le stesse cose che io ho scritto per esteso, in forma dialogica invece che in simboli?
Solo che hai come un blocco...
Le equazioni sono:
T + O = C + S
C + O = 2(T + S)
S + O = 3(T + C)
O = 1320 - T - C - S
#843
Storia / Sintesi estrema della storia dell'architettura (e dell'uomo)
13 Febbraio 2024, 11:42:31 AMI tre più importanti ed imponenti edifici eretti sulla superficie del nostro pianeta, costituiscono, almeno secondo me, la dimostrazione della "vanità", della "crudeltà" e della "inanità" delle aspirazioni umane; in ogni caso, tutte e tre, a mio parere, sono una palese dimostrazione della deprimente "stupidità" dell'uomo.
#844
Varie / Rastislav e l'enigma dei pallini da separare gli uni dagli altri
13 Febbraio 2024, 11:15:24 AMRastislav entra nella cella di un prigioniero, e gli consegna un foglio con sopra disegnati 16 pallini.
***
Poi gli dice:
- Ora tu, con una matita ed un righello, devi separare ciascun pallino dagli altri, tracciando sul foglio, ed attraversandolo da un lato all'altro, il "numero minimo possibile di linee rette" (rectius "segmenti di retta"); facendo, cioè, in modo tale che ciascun pallino risulti "perimetrato" da almeno 3, o più lati, retti, che lo separino dai pallini limitrofi.
Non importa la forma geometrica di tali perimetri, che può essere sia regolare che irregolare; ma nessuna delle rette che traccerai, attraversando il foglio, potrà "intersecare" o anche soltanto "sfiorare" nessun pallino.
Le 4 linee rette che delimitano il foglio possono contribuire a formare i lati di alcuni dei perimetri in cui saranno racchiusi i pallini; esse non verranno calcolate nel "numero minimo possibile di linee rette" (rectius "segmenti di retta") che tu dovrai tracciare per separare i pallini l'uno dall'altro!
Le 4 linee rette che delimitano il foglio possono contribuire a formare i lati di alcuni dei perimetri in cui saranno racchiusi i pallini; esse non verranno calcolate nel "numero minimo possibile di linee rette" (rectius "segmenti di retta") che tu dovrai tracciare per separare i pallini l'uno dall'altro!
Se ci riesci entro stasera, ti renderò la libertà; altrimenti morirai!-
***
Come se la cava il prigioniero?
***
#845
Varie / Re: L'enigma dell'eredità
13 Febbraio 2024, 11:06:32 AMCitazione di: bobmax il 13 Febbraio 2024, 10:33:51 AMIn realtà, Eutidemo, come dato è sufficiente l'importo totale.Ti credo sulla parola, perchè io non sarei mai in grado di eseguire tale operazione
Perché si tratta di risolvere un sistema di 4 equazioni lineari con 4 incognite.
#846
Varie / Re: L'enigma dell'eredità
13 Febbraio 2024, 10:20:08 AMCiao Bobmax.
Come al solito, sei *INSUPERABILE!* 
Ed infatti, come avevo scritto, gli "importi chiave" per risolvere l'enigma, sono:
1)
Il totale dell'asse ereditario, pari a 1.320 euro.
2)
L'importo ricevuto dall'Ospedale.
***
Ciò in quanto, per rispettare le altre condizioni ipotetiche poste dal quesito, tale importo deve necessariamente essere di 605 euro (altrimenti gli altri conti non tornano più).
***
Ed infatti, solo partendo da tali importi come "chiave di lettura", avremo le seguenti quote ereditarie dei tre fratelli:
a)
Caio 55 euro, perchè 605 + 55 = 660 euro, corrispondenti a 275 di Tizio + 385 euro di Sempronio.
b)
Tizio 275 euro, perchè 605 + 275 = 880 euro, corrispondenti a 55 euro di Caio + a 385 euro di Sempronio, moltiplicati per 2 (440 x 2 = 880).
c)
Sempronio 385 euro, perchè 605 + 385 = 990 euro, corrispondenti a 55 euro di Caio + i 275 euro di Tizio , moltiplicati per 3 (330 x 3 = 990).
***
Ed infatti, solo così, potremmo ottenere gli addendi necessari per rispettare le tre ipotesi dell'enigma, ed ottenere un totale di 1.320 euro:
605 + 55 + 275 + 385 = 1.320
***
Complimenti ed un cordiale saluto
***
Complimenti ed un cordiale saluto
***
#847
Varie / Re: L'enigma dell'eredità
13 Febbraio 2024, 06:46:29 AM
Vi do un AIUTINO!
Secondo me, gli "importi chiave" per risolvere l'enigma, sono:
1)
Il totale dell'asse ereditario, pari a 1.320 euro.
2)
L'importo ricevuto dall'Ospedale.
Secondo me, gli "importi chiave" per risolvere l'enigma, sono:
1)
Il totale dell'asse ereditario, pari a 1.320 euro.
2)
L'importo ricevuto dall'Ospedale.
#848
Varie / Re: Rastislav e l'enigma della "E" maiuscola e dell'area del quadrato
12 Febbraio 2024, 12:07:34 PMCiao Bobmax.
Bravissimo!
Io non avevo minimamente riflettuto sul fatto che la diagonale di un rettangolo era proprio il lato di quel quadrato di area 10!
***
Comunque il mio invito a non porvi "limiti inutili", si riferiva al fatto che:
- le sezioni della "E" non potevano essere "ruotate" nello spazio piano per formare un quadrato;
- però il quadrato risultante da tali sezioni "non ruotate", poteva benissimo essere "ruotato", e cioè, non posato per dritto, ma inclinato di lato.
Ed infatti non era affatto prescritto quale dovesse essere l'angolo di inclinazione del quadrato! 
***
Un cordiale saluto!
***
#849
Varie / L'enigma dell'eredità
12 Febbraio 2024, 11:51:02 AMUn povero vecchio ricoverato in ospedale, il cui conto in banca ammontava in tutto a soli 1.320 euro, aveva tre figli; prima di morire lasciò tutto in eredità ai tre figli e all'ospedale, ma (non si sa perchè), ad ognuno in misura diversa.
Per cui i tre figli, di nome Tizio, Caio e Sempronio, e l'ospedale, ricevettero ciascuno una quota differente dell'eredità di 1.320 euro.
***
Ora bisogna indovinare di quale entità era tale quota "pro capite" di ciascuno, tenendo conto di quanto segue:
a)
Se l'importo spettante all'ospedale fosse stato lasciato a Tizio (oltre alla quota a lui destinata), costui avrebbe ereditato un importo pari alla somma dell'eredità ricevuta dagli altri due fratelli.
b)
Se l'importo spettante all'ospedale fosse stato lasciato a Caio (oltre alla quota a lui destinata), costui avrebbe ereditato un importo pari al doppio della somma dell'eredità ricevuta dagli altri due fratelli.
c)
Se l'importo spettante all'ospedale fosse stato lasciato a Sempronio (oltre alla quota a lui destinata), costui avrebbe ereditato un importo pari al triplo della somma dell'eredità ricevuta dagli altri due fratelli.
***
Qual'è l'importo effettivamente ricevuto da ciascuno dei tre fratelli e dall'ospedale!
***
P.S.
Questo enigma, per farmi perdonare, è molto più facile di quello della "E" maiuscola con la stessa area del quadrato; spero solo di non aver sbagliato i calcoli, essendo io una pippa in aritmetica! 
#850
Varie / Re: Rastislav e l'enigma della "E" maiuscola e dell'area del quadrato
12 Febbraio 2024, 11:32:29 AM
Ciao Bobmax.
Peraltro, frazionando ulteriormente la mia soluzione, essa diventa identica alla tua (e viceversa).
Tutto sta se preferiamo scegliere:
- un minor numero di sezioni, una delle quali, però, irregolare;
- un maggior numero di sezioni, però tutte regolari.
***
Alla fin fine la tua soluzione mi piace più della mia; in quanto la trovo molto più "elegante"!
Chapeau!
***
Un cordiale saluto!
***
Peraltro, frazionando ulteriormente la mia soluzione, essa diventa identica alla tua (e viceversa).
Tutto sta se preferiamo scegliere:
- un minor numero di sezioni, una delle quali, però, irregolare;
- un maggior numero di sezioni, però tutte regolari.
***
Alla fin fine la tua soluzione mi piace più della mia; in quanto la trovo molto più "elegante"!
Chapeau!
***
Un cordiale saluto!
***
#851
Varie / Re: Rastislav e l'enigma della "E" maiuscola e dell'area del quadrato
12 Febbraio 2024, 11:21:28 AMCiao Bobmax.
Scusami, ma, avendo tu sovrapposto le due figure, ed avendo omesso di nominare tre sezioni, mi era rimasto arduo capire bene quello che avevi fatto; che, in sostanza, vista la mia concessione sul "numero minimo di sezioni", mi sembra, però, sostanzialmente corretto.
***
Cioè, se ho capito bene ciò che intendevi, scindendo le due figure, avremmo avuto il seguente disegno:
***
Ma, forse, ho capito male quello che intendevi, perchè tu scrivi: "nella mia soluzione vi sono 5 parti sezionate: due triangoli, un quadrato, un rettangolo e una figura irregolare."
Io, invece, nel disegno riproducente la tua soluzione, vedo:
- 7 sezioni;
- tutte costituite da figure geometriche regolari, cioè, 4 triangoli scaleni, 2 quadrati e 1 rettangolo.
***
La mia soluzione, invece, era la seguente:
Cioè:
- 5 sezioni;
- composte, come vi avevo rivelato in precedenza, da 2 triangoli, da 1 quadrato, da 1 rettangolo e da 1 figura geometrica irregolare.
***
In ogni caso, a parte il "numero minimo di sezioni" (che vi avevo condonato), dopo averla esaminata meglio, mi sembra che la tua soluzione sia del tutto corretta.
Per cui, COMPLIMENTI...sei stato BRAVISSIMO! 
***
Un cordiale saluto!
***
#852
Varie / Re: Rastislav e l'enigma della "E" maiuscola e dell'area del quadrato
12 Febbraio 2024, 07:35:47 AM
Ciao Bobmax.
***
Fuochissimo
Ma fai ancora un piccolo sforzo!
***
Un cordiale saluto!
***
***
Fuochissimo
Ma fai ancora un piccolo sforzo!
***
Un cordiale saluto!
***
#853
Varie / Re: Rastislav e l'enigma della "E" maiuscola e dell'area del quadrato
12 Febbraio 2024, 06:11:29 AM
Dai, sono convinto che ci siete quasi!!!
#854
Varie / Re: Rastislav e l'enigma della "E" maiuscola e dell'area del quadrato
12 Febbraio 2024, 06:09:52 AMCitazione di: iano il 11 Febbraio 2024, 19:56:20 PMToglierei la seguente condizione:Va bene, accordato!
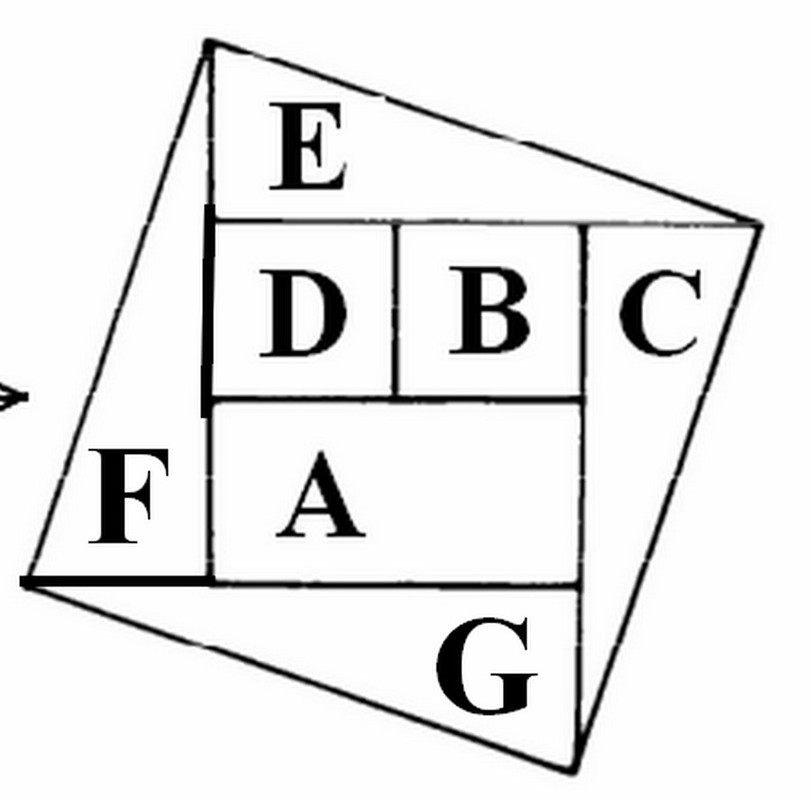
''Ora tu, con un righello, devi dividere questa "E" nel "numero minimo possibile"di sezioni''
perchè diversamente la soluzione dovrebbe contenere anche la dimostrazione che abbiamo trovato ''il numero minimo possibile''.
Non è necessaria anche la dimostrazione che abbiate trovato ''il numero minimo possibile'' di sezioni.
#855
Varie / Re: Rastislav e l'enigma della "E" maiuscola e dell'area del quadrato
12 Febbraio 2024, 06:06:51 AMCitazione di: bobmax il 11 Febbraio 2024, 16:10:44 PMI tre rettangoli hanno le stesse dimensioni?Sì!