
Enciclopedia Indice
Archita di Taranto
Archita di Taranto (gr. Archýtas) matematico, stratego e filosofo greco (Taranto ca. 428-347 a. C.). Ultimo rappresentante del pensiero pitagorico e austero uomo politico, resse per lungo tempo le sorti della sua città incrementandone la prosperità e la potenza e facendone la prima della Magna Grecia. In campo matematico e filosofico, continuò la tradizione pitagorica che anteponeva l'aritmetica alla geometria, pur utilizzando le più differenti tecniche nella risoluzione di complessi problemi matematici. Teorico di musica, derivò dallo studio del rapporto fra suoni armonici il concetto del numero inteso essenzialmente come rapporto, indipendente quindi dai vincoli di commensurabilità e razionalità. Altro problema prettamente aritmetico, espresso geometricamente come duplicazione del cubo (problema di Delo), fu risolto da Archita con un metodo insieme meccanico e di geometria spaziale. Fu infatti il primo e per lungo tempo l'unico filosofo della Grecia classica a intuire i vantaggi di un collegamento fra matematica e meccanica; gli si attribuiscono l'invenzione della raganella (strumento musicale) e la costruzione di una colomba volante di legno e di altri dispositivi meccanici. Ancora dai suoi studi di matematica applicata alla meccanica ricavò le nozioni che il suono è dovuto al movimento e all'urto fra corpi e che esiste un legame fra intensità della vibrazione e altezza di un suono. Amico di Platone, che fu vivamente influenzato dal suo pensiero, si adoperò per la sua liberazione dopo i contrasti che il grande filosofo ateniese ebbe a Siracusa con Dionisio II.
Curva di Archita
La prima curva gobba (cioè non contenuta in alcun piano) che si incontra nella storia della matematica, introdotta da Archita per risolvere il problema della duplicazione del cubo. Alla sua equazione si arriva nel seguente modo: dati due segmenti a, b siano u e v i loro medi proporzionali, cioè sia a:u= =u:v=v:b.
Se si pone
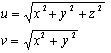
sostituendo questi valori nella proporzione si ricavano le seguenti relazioni:
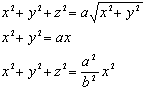
che sono equazioni di superfici. La prima è un toro, le altre due sono un cilindro e un cono quadrici che si incontrano lungo una linea di quart'ordine che costituisce la curva di Archita. Se si proietta questa curva sul piano xy, la sua equazione in coordinate polari r e J è la seguente:
![]()
essa costituisce una curva detta campila di Eudosso.
Libri pubblicati da Riflessioni.it
RIFLESSIONI SUL SENSO DELLA VITA 365 MOTIVI PER VIVERE |



